Niet iedereen weet dat de atmosferische druk op verschillende hoogten anders is. Er is zelfs een speciaal apparaat om zowel druk als hoogte te meten. Het wordt een barometer-hoogtemeter genoemd. In het artikel zullen we in detail bestuderen hoe de atmosferische druk verandert met de hoogte en wat de luchtdichtheid ermee te maken heeft. Laten we eens kijken naar deze afhankelijkheid van het voorbeeld van een grafiek.
Atmosferische druk op verschillende hoogten

De atmosferische druk hangt af van de hoogte. Wanneer deze met 12 m wordt verhoogd, neemt de druk af met 1 mm Hg. Dit feit kan worden geschreven met de volgende wiskundige uitdrukking: ∆h/∆P=12 m/mm Hg. Kunst. ∆h is de verandering in hoogte, ∆P is de verandering in atmosferische druk met een verandering in hoogte met ∆h. Wat volgt hieruit?
De formule laat zien hoe de atmosferische druk verandert met de hoogte. Dus als we met 12 m stijgen, da alt de bloeddruk met 12 mm Hg, als met 24 m - danbij 2 mmHg. Dus door de atmosferische druk te meten, kan men de hoogte beoordelen.
Millimeters kwik en hectopascals
Bij sommige problemen wordt de druk niet uitgedrukt in millimeters kwik, maar in pascal of hectopascal. Laten we de bovenstaande relatie schrijven voor het geval dat de druk wordt uitgedrukt in hectopascals. 1 mmHg Kunst.=133,3 Pa=1,333 hPa.
Laten we nu de verhouding tussen hoogte en atmosferische druk uitdrukken, niet in millimeters kwik, maar in hectopascals. ∆h/∆P=12 m/1, 333 hPa. Na berekening krijgen we: ∆h/∆P=9 m/hPa. Het blijkt dat wanneer we 9 meter stijgen, de druk met één hectopascal afneemt. De normale druk is 1013 hPa. Laten we 1013 naar 1000 afronden en aannemen dat dit precies de BP op het aardoppervlak is.
Als we 90 meter klimmen, hoe verandert de atmosferische druk dan met de hoogte? Het neemt af met 10 hPa, met 90 m - met 100 hPa, met 900 m - met 1000 hPa. Als de druk op de grond 1000 hPa is, en we klommen 900 m omhoog, dan werd de atmosferische druk nul. Dus het blijkt dat de atmosfeer eindigt op negen kilometer hoogte? Nee. Op zo'n hoogte is er lucht, daar vliegen vliegtuigen. Dus wat is er aan de hand?
Relatie tussen luchtdichtheid en hoogte. Functies

Hoe verandert de atmosferische druk met de hoogte nabij het aardoppervlak? Bovenstaande foto heeft deze vraag al beantwoord. Hoe hoger de hoogte, hoe lager de luchtdichtheid. Zolang we ons dicht bij het aardoppervlak bevinden, is de verandering in luchtdichtheid niet waarneembaar. Daarom, voor elkper hoogte-eenheid neemt de druk met ongeveer dezelfde waarde af. De twee uitdrukkingen die we eerder opschreven, moeten alleen als correct worden beschouwd als we ons dicht bij het aardoppervlak bevinden, niet hoger dan 1-1,5 km.
Een grafiek die laat zien hoe de atmosferische druk verandert met de hoogte
Laten we nu verder gaan met zichtbaarheid. Laten we een grafiek maken van atmosferische druk versus hoogte. Op nul hoogte P0=760 mm Hg. Kunst. Vanwege het feit dat met toenemende hoogte de druk afneemt, zal atmosferische lucht minder worden gecomprimeerd en zal de dichtheid ervan afnemen. Daarom zal in de grafiek de afhankelijkheid van druk en hoogte niet worden beschreven door een rechte lijn. Wat betekent dit?
Hoe verandert de atmosferische druk met de hoogte? Boven de grond? Op een hoogte van 5,5 km neemt deze 2 keer af (Р0/2). Het blijkt dat als we naar dezelfde hoogte stijgen, dat wil zeggen 11 km, de druk met nog eens de helft zal afnemen en gelijk zal zijn aan Р0/4, enz.
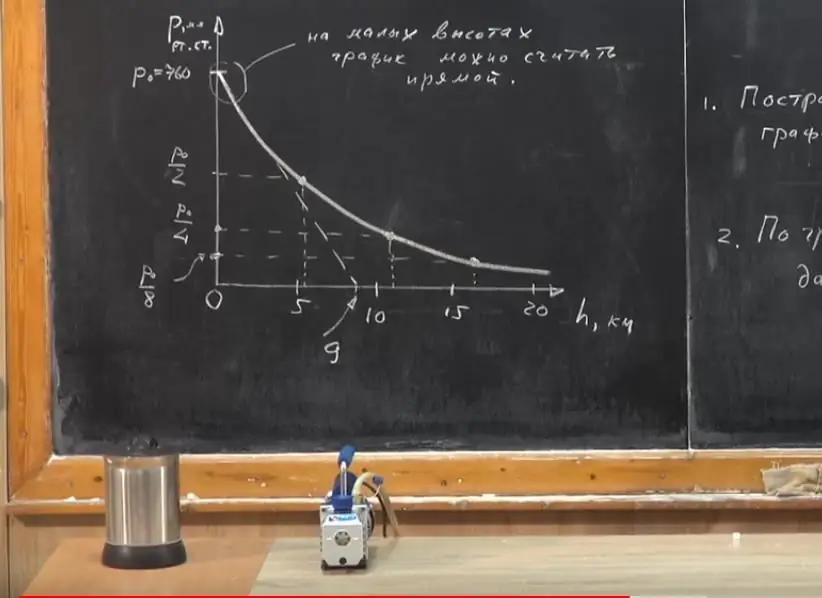
Laten we de punten met elkaar verbinden en we zullen zien dat de grafiek geen rechte lijn is, maar een kromme. Waarom, toen we de afhankelijkheidsrelatie opschreven, leek het alsof de atmosfeer eindigt op een hoogte van 9 km? We hebben overwogen dat de grafiek op elke hoogte recht is. Dit zou het geval zijn als de atmosfeer vloeibaar was, dat wil zeggen als de dichtheid constant was.
Het is belangrijk om te begrijpen dat deze grafiek slechts een fragment is van de afhankelijkheid op lage hoogten. Op geen enkel punt op deze lijn da alt de druk tot nul. Zelfs in de verre ruimte zijn er gasmoleculen, die echter geenrelatie tot de atmosfeer van de aarde. Er is geen absoluut vacuüm, leegte in geen enkel punt van het heelal.






