Er zijn objecten die in staat zijn om de dichtheid van de elektromagnetische stralingsflux die erop v alt te veranderen, dat wil zeggen, ofwel vergroten door het op een bepaald punt te verzamelen, ofwel te verminderen door het te verstrooien. Deze objecten worden in de natuurkunde lenzen genoemd. Laten we dit probleem eens nader bekijken.
Wat zijn lenzen in de natuurkunde?
Dit concept betekent absoluut elk object dat in staat is om de voortplantingsrichting van elektromagnetische straling te veranderen. Dit is de algemene definitie van lenzen in de natuurkunde, waaronder optische glazen, magnetische en zwaartekrachtlenzen.
In dit artikel ligt de focus op optische glazen, dit zijn objecten gemaakt van transparant materiaal en beperkt door twee oppervlakken. Een van deze oppervlakken moet noodzakelijkerwijs een kromming hebben (dat wil zeggen, deel uitmaken van een bol met een eindige straal), anders zal het object niet de eigenschap hebben om de voortplantingsrichting van lichtstralen te veranderen.
Het principe van de lens

De essentie van het werk van deze ongecompliceerdeoptisch object is het fenomeen van breking van de zonnestralen. Aan het begin van de 17e eeuw publiceerde de beroemde Nederlandse natuurkundige en astronoom Willebrord Snell van Rooyen de brekingswet, die momenteel zijn achternaam draagt. De formulering van deze wet is als volgt: wanneer zonlicht door het grensvlak tussen twee optisch transparante media gaat, dan is het product van de sinus van de invalshoek tussen de bundel en de normaal op het oppervlak en de brekingsindex van het medium waarin het propageert is een constante waarde.

Om het bovenstaande te verduidelijken, laten we een voorbeeld geven: laat het licht op het wateroppervlak vallen, terwijl de hoek tussen de normaal op het oppervlak en de straal θ1 is. Dan wordt de lichtstraal gebroken en begint zijn voortplanting in het water al onder een hoek θ2 met de normaal op het oppervlak. Volgens de wet van Snellius krijgen we: sin(θ1)n1=sin(θ2) n2, waarbij n1 en n2 de brekingsindices zijn voor lucht en water, respectievelijk. Wat is de brekingsindex? Dit is een waarde die aangeeft hoe vaak de voortplantingssnelheid van elektromagnetische golven in vacuüm groter is dan die voor een optisch transparant medium, dat wil zeggen n=c/v, waarbij c en v de lichtsnelheden in vacuüm en in de gemiddeld, respectievelijk.
De fysica van het optreden van breking ligt in de implementatie van het principe van Fermat, volgens welke licht zo beweegt dat de afstand van het ene punt naar het andere in de ruimte in de kortst mogelijke tijd wordt overbrugd.
Typen lenzen

Het type optische lens in de natuurkunde wordt uitsluitend bepaald door de vorm van de oppervlakken die het vormen. De brekingsrichting van de daarop invallende bundel hangt af van deze vorm. Dus als de kromming van het oppervlak positief (convex) is, zal de lichtstraal bij het verlaten van de lens zich dichter bij zijn optische as voortplanten (zie hieronder). Omgekeerd, als de kromming van het oppervlak negatief (concaaf) is en door het optische glas gaat, zal de straal van zijn centrale as af bewegen.
Merk nogmaals op dat een oppervlak met een kromming stralen op dezelfde manier breekt (volgens de wet van Stella), maar de normalen daarvoor hebben een andere helling ten opzichte van de optische as, wat resulteert in een ander gedrag van de gebroken straal.
Een lens die wordt begrensd door twee convexe oppervlakken wordt een convergerende lens genoemd. Als het op zijn beurt wordt gevormd door twee oppervlakken met negatieve kromming, wordt het verstrooiing genoemd. Alle andere soorten optische glazen worden geassocieerd met een combinatie van deze oppervlakken, waaraan ook een vlak wordt toegevoegd. Welke eigenschap de gecombineerde lens zal hebben (divergent of convergerend) hangt af van de totale kromming van de stralen van zijn oppervlakken.
Lenselementen en straaleigenschappen

Om lenzen in beeldfysica in te bouwen, moet je kennis maken met de elementen van dit object. Ze worden hieronder vermeld:
- Hoofd optische as en centrum. In het eerste geval bedoelen ze een rechte lijn die loodrecht op de lens loopt door zijn optische middelpunt. Dit laatste is op zijn beurt een punt in de lens waar de straal doorheen gaat en geen breking ervaart.
- Brandpuntsafstand en focus - de afstand tussen het middelpunt en een punt op de optische as, die alle stralen verzamelt die op de lens vallen evenwijdig aan deze as. Deze definitie geldt voor het verzamelen van optische glazen. In het geval van divergente lenzen zijn het niet de stralen zelf die in een punt samenkomen, maar hun denkbeeldige voortzetting. Dit punt wordt het hoofdfocus genoemd.
- Optisch vermogen. Dit is de naam van het omgekeerde van de brandpuntsafstand, dat wil zeggen D \u003d 1 / f. Het wordt gemeten in dioptrieën (dioptrieën), dat wil zeggen 1 dioptrie.=1 m-1.
Dit zijn de belangrijkste eigenschappen van de stralen die door de lens gaan:
- straal die door het optische centrum gaat, verandert zijn bewegingsrichting niet;
- stralen die evenwijdig aan de optische hoofdas invallen, veranderen van richting zodat ze door het hoofdfocus gaan;
- stralen die onder elke hoek op optisch glas vallen, maar door het brandpunt gaan, veranderen hun voortplantingsrichting op zo'n manier dat ze evenwijdig worden aan de optische hoofdas.
De bovenstaande eigenschappen van stralen voor dunne lenzen in de natuurkunde (zoals ze worden genoemd omdat het niet uitmaakt welke bollen ze worden gevormd en hoe dik ze ook zijn, alleen de optische eigenschappen van de materie van het object) worden gebruikt om er afbeeldingen in te bouwen.
Beelden in optische glazen: hoe te bouwen?
Hieronder is een figuur die de schema's beschrijft voor het construeren van afbeeldingen in de convexe en concave lenzen van een object(rode pijl) afhankelijk van de positie.
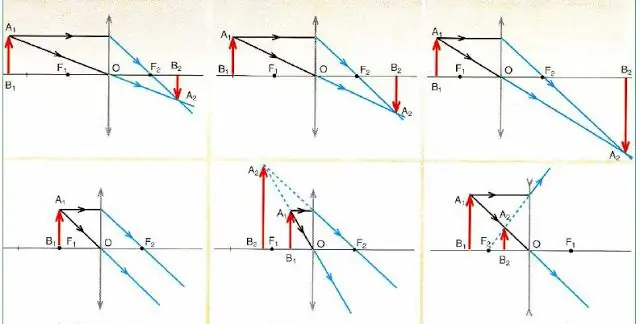
Belangrijke conclusies volgen uit de analyse van de circuits in de figuur:
- Elk beeld is gebouwd op slechts 2 stralen (die door het midden gaan en evenwijdig aan de optische hoofdas).
- Convergerende lenzen (aangegeven met pijlen aan de uiteinden die naar buiten wijzen) kunnen zowel een vergroot als verkleind beeld geven, dat op zijn beurt echt (echt) of denkbeeldig kan zijn.
- Als het object scherp is, vormt de lens zijn beeld niet (zie het onderste diagram links in de afbeelding).
- Verstrooiende optische glazen (aangegeven door pijlen aan de uiteinden die naar binnen wijzen) geven altijd een gereduceerd en virtueel beeld, ongeacht de positie van het object.
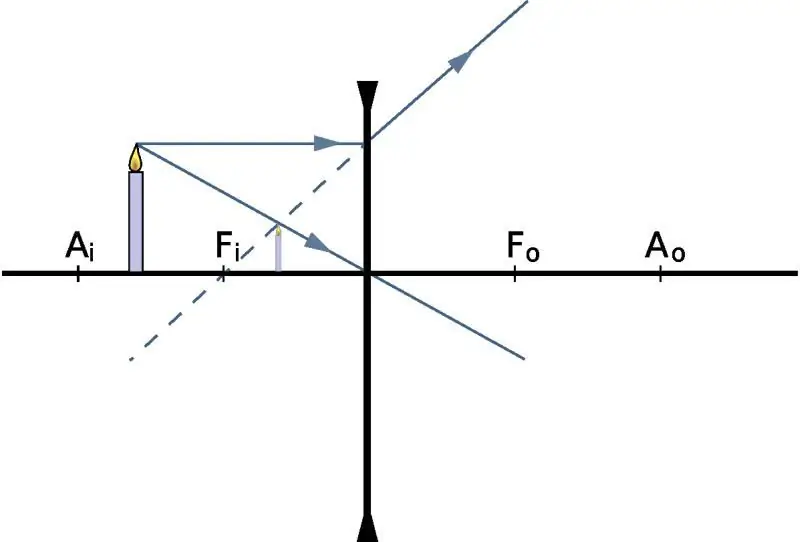
De afstand tot een afbeelding zoeken
Om te bepalen op welke afstand het beeld zal verschijnen, als we de positie van het object zelf kennen, geven we de lensformule in de natuurkunde: 1/f=1/do + 1 /d i, waarbij do en di de afstand zijn tot het object en zijn beeld vanaf de optische centrum, respectievelijk f is de belangrijkste focus. Als we het hebben over een verzamelend optisch glas, dan is het f-getal positief. Omgekeerd, voor een divergente lens, is f negatief.
Laten we deze formule gebruiken om een eenvoudig probleem op te lossen: laat het object zich op een afstand do=2f van het midden van het verzamelende optische glas bevinden. Waar zal zijn afbeelding verschijnen?
Van de toestand van het probleem hebben we: 1/f=1/(2f)+1/di. Van: 1/di=1/f - 1/(2f)=1/(2f), d.w.z. di=2 f. Het beeld zal dus verschijnen op een afstand van twee brandpunten van de lens, maar aan de andere kant dan het object zelf (dit wordt aangegeven door het positieve teken van de waarde di).
Een korte geschiedenis
Het is merkwaardig om de etymologie van het woord "lens" te geven. Het komt van de Latijnse woorden lens en lentis, wat "linze" betekent, aangezien optische objecten in hun vorm echt op de vrucht van deze plant lijken.
De brekingskracht van sferische transparante lichamen was bekend bij de oude Romeinen. Hiervoor gebruikten ze ronde glazen vaten gevuld met water. Glazen lenzen zelf werden pas in de 13e eeuw in Europa gemaakt. Ze werden gebruikt als leesinstrument (moderne bril of vergrootglas).
Het actieve gebruik van optische objecten bij de vervaardiging van telescopen en microscopen dateert uit de 17e eeuw (aan het begin van deze eeuw vond Galileo de eerste telescoop uit). Merk op dat de wiskundige formulering van Stella's brekingswet, zonder kennis waarvan het onmogelijk is om lenzen met de gewenste eigenschappen te vervaardigen, aan het begin van dezelfde 17e eeuw door een Nederlandse wetenschapper werd gepubliceerd.
Andere lenzen
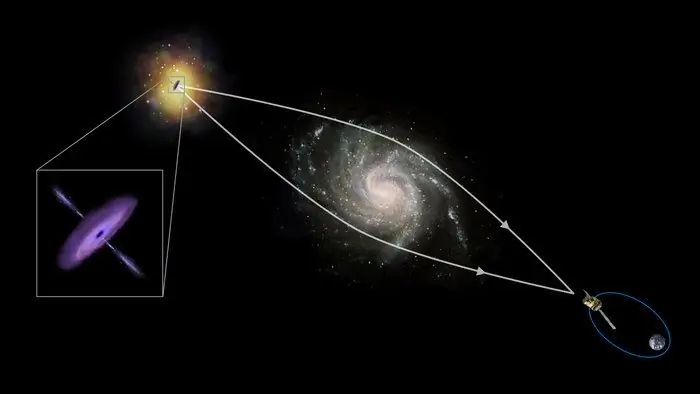
Zoals hierboven opgemerkt, zijn er naast optische brekende objecten ook magnetische en zwaartekrachtsobjecten. Een voorbeeld van het eerste zijn magnetische lenzen in een elektronenmicroscoop, een levendig voorbeeld van het laatste is de vervorming van de richting van de lichtstroom,wanneer het langs massieve ruimtelichamen (sterren, planeten) komt.






