Piramide samen met een prisma is een perfect veelvlak in de driedimensionale ruimte, hun geometrische kenmerken worden bestudeerd op de middelbare school. In dit artikel zullen we bekijken wat piramides zijn, uit welke elementen ze bestaan, en ook kort de juiste piramides karakteriseren.
Geometrische figuur piramide
Vanuit het oogpunt van geometrie is de piramide een ruimtelijke figuur, bestaande uit een veelhoek en verschillende driehoeken. Het verkrijgen van dit cijfer is vrij eenvoudig. Om dit te doen, neem je een veelhoek met n zijden, kies je een willekeurig punt in de ruimte dat niet in het vlak van de veelhoek zal liggen, en verbind je elk hoekpunt van de veelhoek met dit punt. Het is duidelijk dat de op deze manier gevormde figuur n driehoeken heeft die op één hoekpunt met elkaar zijn verbonden.
Laten we een foto maken om de geometrische vorm van de beschreven figuur te visualiseren.

Dit toont een vierhoekige piramide, waarvan de basis isvierhoek, en het zijoppervlak wordt gevormd door vier driehoeken die een gemeenschappelijk hoekpunt hebben.
Piramide elementen
Zoals elk veelvlak, wordt de piramide gevormd door drie soorten elementen:
- randen;
- tops;
- ribben.
Gezichten zijn delen van vlakken die het interne volume van een figuur scheiden van de omringende ruimte. Als de basis van de piramide een n-gon bevat, dan is het aantal vlakken altijd n+1. Hiervan zijn n zijden driehoekig en één zijde is de genoemde n-gonale basis.
Vertices zijn punten waar drie of meer vlakken van een figuur elkaar snijden. Het basisgebied bevat n hoekpunten, die elk worden gevormd door twee driehoekige vlakken en een basis. Het punt waar n driehoekige zijden samenkomen, wordt de top van de piramide genoemd. De beschouwde figuur bestaat dus uit n+1 hoekpunten.
Randen zijn rechte lijnen die verschijnen wanneer twee vlakken elkaar kruisen. Elke rand wordt aan de uiteinden begrensd door twee hoekpunten. Elke piramide met een n-gon basis bevat 2n randen. De helft van dit aantal, dat wil zeggen n, wordt uitsluitend gevormd door het snijpunt van zijdriehoeken.
Mogelijke soorten figuren
De naam van de figuur in kwestie wordt op unieke wijze bepaald door het type polygoon aan de basis. Als het bijvoorbeeld drie hoeken en drie zijden heeft, is de piramide driehoekig, als vier vierhoekig, enzovoort.
Polygoon kan convex en concaaf zijn, evenals regelmatig en algemeen type. Dit alles bepa alt ook het uiterlijk van de piramide.
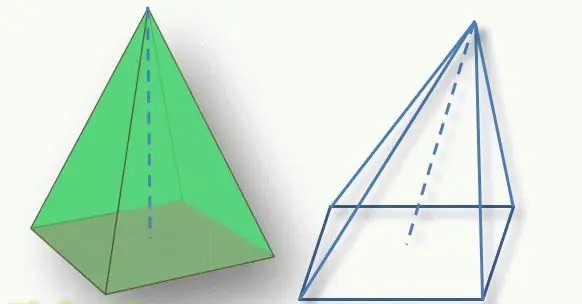
Een belangrijk punt bij het bepalen van het type figuur is de positie van de top van de piramide ten opzichte van de basis. Het loodrechte segment dat van de bovenkant naar de veelhoekige basis wordt getrokken, wordt de hoogte van de figuur genoemd. Als dit segment de basis snijdt in zijn geometrische middelpunt (voor een driehoek is dit het snijpunt van medianen, voor een vierhoek het snijpunt van diagonalen), dan wordt de figuur een rechte lijn genoemd. Anders spreken ze van een hellende piramide.
Als de n-hoek van de basis regelmatig is (gelijkzijdige driehoek, vierkant, enz.), en de figuur is recht, dan wordt het een regelmatige piramide genoemd.
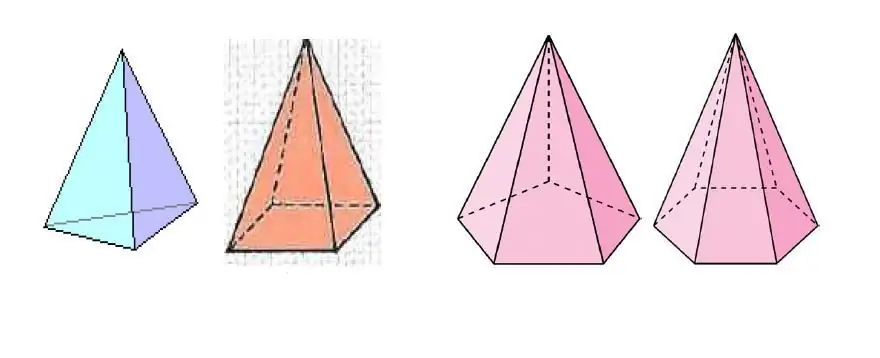
De afbeelding hierboven toont verschillende piramides, die verschillen in het aantal zijden van de veelhoek aan de basis.
Eigenschappen van reguliere piramides
Deze piramides verschillen van andere figuren van deze klasse door een hoge mate van symmetrie. In dit opzicht is het handig om er verschillende geometrische berekeningen mee uit te voeren, bijvoorbeeld volume of oppervlakte.
Een gewone piramide bevat een n-gon aan de basis, waarvan het gebied uniek wordt bepaald op basis van de kennis van de lengte van zijn zijde. Het laterale oppervlak van de figuur wordt gevormd door n identieke driehoeken, die gelijkzijdig zijn. De randen van een regelmatige piramide op het zijoppervlak zijn gelijk aan elkaar. De waarde van de lengte van deze rand wordt vaak gebruikt bij het berekenen van het apothema van een figuur en het bepalen van de oppervlakte.
De hoogte van een regelmatige piramide is het tweede belangrijke kenmerk van de figuur (de eerste is de lengte van de rand)gronden). Hoogte wordt gebruikt bij het berekenen van het volume.
Elk vlak evenwijdig aan de basis, dat de zijvlakken van de piramide snijdt, leidt tot de vorming van een veelhoekige sectie. Het is homothetisch met betrekking tot de basispolygoon. De beschreven slice-operatie leidt tot de vorming van een hele klasse nieuwe figuren - afgeknotte regelmatige piramides.
De beroemdste piramides

Natuurlijk zijn dit de regelmatige vierhoekige piramides van de Egyptische farao's. In een plaats genaamd Gizeh zijn er meer dan 100 van deze stenen monumenten, waarvan de perfectie van ontwerp en de nauwkeurigheid van de geometrische parameters wetenschappers tot op de dag van vandaag verbazen. De grootste daarvan is de Piramide van Cheops, die ongeveer 146 meter hoog en ongeveer 230 meter lang is.
Waar deze piramides precies voor dienden, en door welke mechanismen en wanneer ze werden gebouwd, weet tot op de dag van vandaag niemand.






