Gassen worden, vanuit het oogpunt van de thermodynamica, beschreven door een reeks macroscopische kenmerken, waarvan de belangrijkste temperatuur, druk en volume zijn. De constantheid van een van deze parameters en de verandering in de andere twee geeft aan dat een of ander isoproces in het gas plaatsvindt. We zullen dit artikel wijden aan een gedetailleerd antwoord op de vragen dat dit een isochoor proces is, hoe het verschilt van isotherme en isobare veranderingen in de toestanden van een gassysteem.
Ideaal gas in de natuurkunde

Voordat u de vraag beantwoordt dat dit een isochoor proces is, moet u het concept van een ideaal gas beter leren kennen. In de natuurkunde wordt het opgevat als elk gas waarin de gemiddelde kinetische energie van de samenstellende deeltjes veel groter is dan de potentiële energie van hun interactie, en de afstanden tussen deze deeltjes zijn enkele ordes van grootte groter dan hun lineaire afmetingen. Onder de genoemde voorwaarden is het mogelijk, bij het uitvoeren vanberekeningen houden geen rekening met de interactie-energie tussen deeltjes (deze is gelijk aan nul), en er kan ook worden aangenomen dat de deeltjes materiële punten zijn met een bepaalde massa m.
Het enige proces dat plaatsvindt in een ideaal gas is de botsing van deeltjes met de wanden van het vat dat de stof bevat. Deze botsingen manifesteren zich in de praktijk als het bestaan van een bepaalde druk in het gas P.
In de regel kan elke gasvormige stof die bestaat uit relatief chemisch inerte moleculen en die een lage druk en hoge temperatuur heeft, worden beschouwd als een ideaal gas met voldoende nauwkeurigheid voor praktische berekeningen.
Vergelijking die een ideaal gas beschrijft
Natuurlijk hebben we het over de universele wet van Clapeyron-Mendelejev, die goed moet worden begrepen om te begrijpen dat dit een isochoor proces is. De universele toestandsvergelijking heeft dus de volgende vorm:
PV=nRT.
Dat wil zeggen, het product van de druk P en het gasvolume V is gelijk aan het product van de absolute temperatuur T en de hoeveelheid stof in mol n, waarbij R de evenredigheidsfactor is. De vergelijking zelf werd voor het eerst opgeschreven door Emile Clapeyron in 1834, en in de jaren 70 van de 19e eeuw verving D. Mendeleev daarin een reeks constante waarden van een enkele universele gasconstante R (8,314 J/(molK))).
In overeenstemming met de Clapeyron-Mendelejev-vergelijking blijft het aantal gasdeeltjes in een gesloten systeem constant, dus er zijn slechts drie macroscopische parameters die kunnen veranderen (T, Pen V). Dit laatste feit ligt ten grondslag aan het begrip van de verschillende isoprocessen die hieronder zullen worden besproken.
Wat is een isochoor proces?
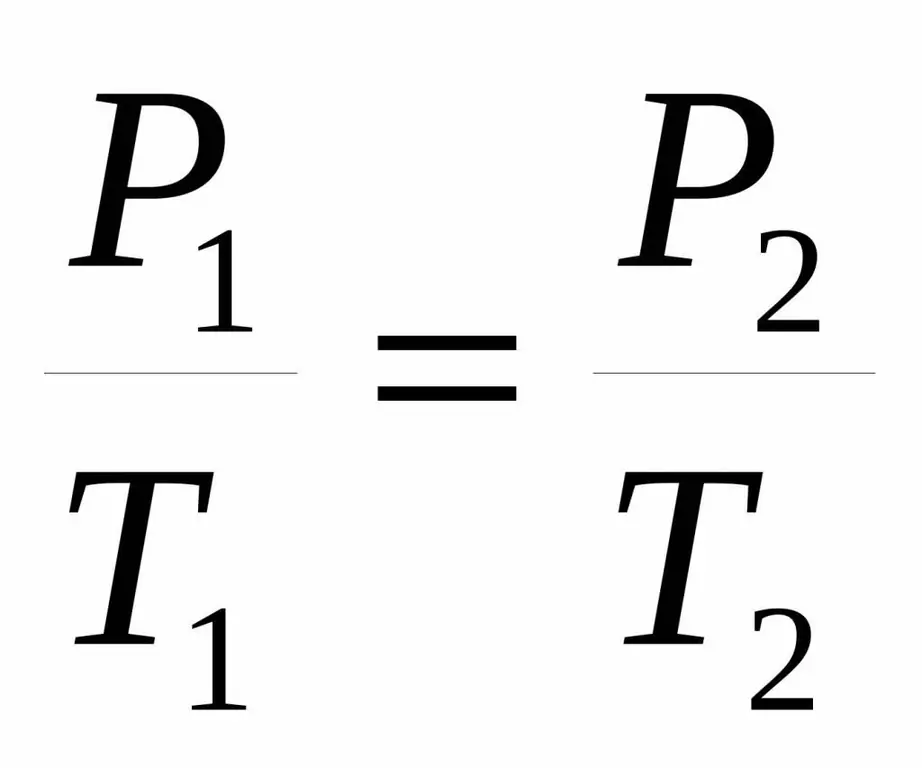
Dit proces wordt gezien als absoluut elke verandering in de toestand van het systeem, waarbij het volume behouden blijft.
Als we ons wenden tot de universele toestandsvergelijking, kunnen we zeggen dat in een isochoor proces alleen druk en absolute temperatuurverandering in een gas. Om precies te begrijpen hoe de thermodynamische parameters veranderen, schrijven we de bijbehorende wiskundige uitdrukking:
P / T=const.
Soms wordt deze gelijkheid in een iets andere vorm gegeven:
P1 / T1=P2 / T 2.
Beide gelijkheden worden de wet van Charles genoemd naar de naam van een Franse wetenschapper die aan het einde van de 18e eeuw de bekende afhankelijkheid experimenteel verkreeg.

Als we een grafiek maken van de functie P(T), dan krijgen we een lineaire afhankelijkheid, die een isochoor wordt genoemd. Elke isochoor (voor alle waarden van n en V) is een rechte lijn.
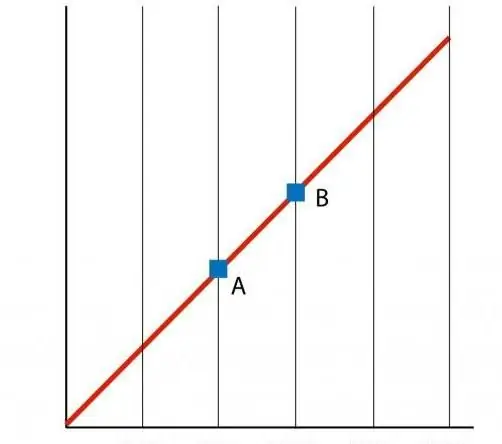
Energiebeschrijving van het proces
Zoals opgemerkt, is een isochoor proces een verandering in de toestand van een systeem die plaatsvindt in een gesloten maar niet geïsoleerd systeem. We hebben het over de mogelijkheid van warmte-uitwisseling tussen het gas en de omgeving. Over het algemeen leidt elke toevoer van warmte Q naar het systeem tot twee resultaten:
- verandert interne energie U;
- gaswerkt A, uitzettend of inkrimpend.
De laatste gevolgtrekking is wiskundig als volgt geschreven:
Q=U + A.
Het isochore proces van een ideaal gas houdt per definitie geen arbeid in die door het gas wordt verricht, aangezien het volume onveranderd blijft. Dit betekent dat alle warmte die aan het systeem wordt geleverd, zijn interne energie gaat verhogen:
Q=U.
Als we de expliciete formule voor interne energie in deze uitdrukking vervangen, dan kan de warmte van het isochore proces worden weergegeven als:
Q=z / 2nRT.
Hier is z het aantal vrijheidsgraden, dat wordt bepaald door de polyatomaire aard van de moleculen waaruit het gas bestaat. Voor een een-atomisch gas, z=3, voor een twee-atomig gas - 5, en voor een drie-atomisch gas en meer - 6. Hier, onder vrijheidsgraden, bedoelen we translatie- en rotatiegraden.
Als we de efficiëntie van het verwarmen van een gassysteem vergelijken in isochore en isobare processen, dan krijgen we in het eerste geval de maximale efficiëntie, omdat tijdens de isobare verandering in de toestand van het systeem het gas uitzet, en een deel van de warmte-inbreng wordt besteed aan het doen van werk.
Isobaar proces
Hierboven hebben we in detail beschreven dat dit een isochoor proces is. Laten we nu een paar woorden zeggen over andere isoprocessen. Laten we beginnen met isobaar. Op basis van de naam wordt het begrepen als de overgang van het systeem tussen toestanden bij constante druk. Dit proces wordt door de Gay-Lussac-wet als volgt beschreven:
V / T=const.
Net als bij de isochoor, vertegenwoordigt de V(T)-isobaar ook een rechte lijn in de grafiek.
Voorvan elk isobaar proces is het handig om de arbeid van het gas te berekenen, aangezien dit gelijk is aan het product van constante druk en de verandering in volume.
Isotherm proces
Dit is een proces waarbij de temperatuur van het systeem constant blijft. Het wordt beschreven door de wet van Boyle-Mariotte voor een ideaal gas. Het is merkwaardig op te merken dat dit de eerste experimenteel ontdekte gaswet is (tweede helft van de 17e eeuw). De wiskundige notatie ziet er als volgt uit:
PV=const.
Isochore en isotherme processen verschillen in hun grafische weergave, aangezien de functie P(V) een hyperbolische, geen lineaire relatie is.
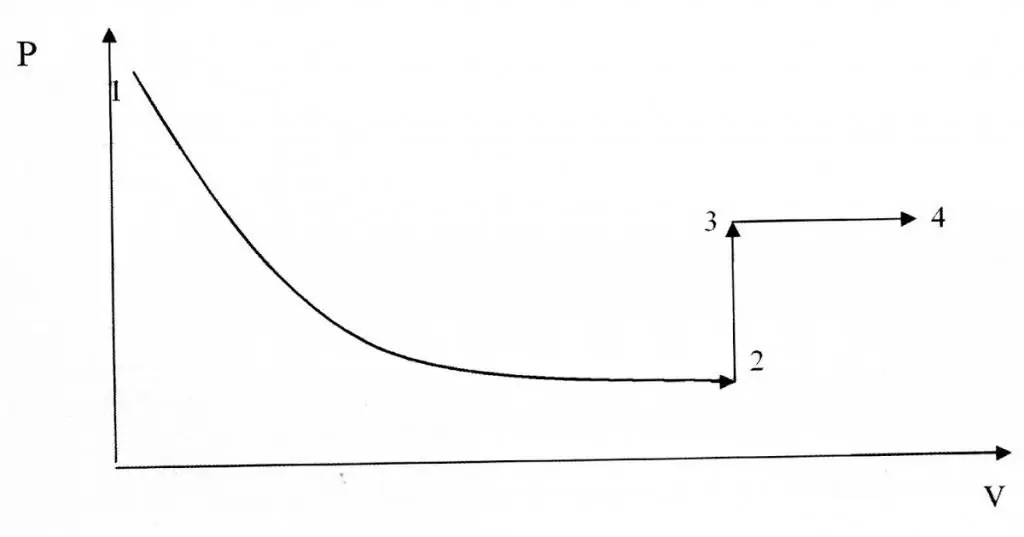
Voorbeeld van probleemoplossing
Laten we de theoretische informatie in het artikel consolideren door hun toepassing om een praktisch probleem op te lossen. Het is bekend dat zuivere gasvormige stikstof zich in een cilinder bevond bij een druk van 1 atmosfeer en een temperatuur van 25°C. Nadat de gasfles was verwarmd en de druk erin was gemeten, bleek deze 1,5 atmosfeer te zijn. Wat is de temperatuur van het gas in de cilinder na verwarming? In welke mate veranderde de interne energie van het gas als er 4 mol stikstof in de ballon zat.
Om de eerste vraag te beantwoorden, gebruiken we de volgende uitdrukking:
P1 / T1=P2 / T 2.
Waar komen we vandaan:
T2=P2 / P1 T 1.
In deze uitdrukking kan druk worden vervangen in willekeurige eenhedenmetingen, omdat ze krimpen en de temperatuur alleen in kelvin is. Dat gezegd hebbende, krijgen we:
T2=1.5 /1298.15=447.224 K.
De berekende temperatuur in graden Celsius is 174 °C.
Aangezien het stikstofmolecuul diatomisch is, kan de verandering in zijn interne energie tijdens verwarming als volgt worden bepaald:
ΔU=5 / 2nRΔT.
Door de bekende waarden in deze uitdrukking in te vullen, krijgen we het antwoord op de tweede vraag van het probleem: ΔU=+12,4 kJ.






