Typische lichteffecten die iedereen in het dagelijks leven vaak tegenkomt, zijn reflectie en breking. In dit artikel zullen we het geval bekijken waarin beide effecten zich manifesteren binnen hetzelfde proces, we zullen het hebben over het fenomeen interne totale reflectie.
Lichtreflectie
Alvorens het fenomeen van interne totale reflectie van licht in overweging te nemen, moet u vertrouwd raken met de effecten van gewone reflectie en breking. Laten we beginnen met de eerste. Voor de eenvoud zullen we alleen licht beschouwen, hoewel deze verschijnselen kenmerkend zijn voor een golf van welke aard dan ook.
Reflectie wordt opgevat als een verandering van een rechtlijnige baan, waarlangs een lichtstraal beweegt, naar een andere rechtlijnige baan, wanneer deze onderweg een obstakel tegenkomt. Dit effect kan worden waargenomen wanneer een laserpointer op een spiegel wordt gericht. Het verschijnen van afbeeldingen van de lucht en bomen wanneer we naar het wateroppervlak kijken, is ook het resultaat van de weerkaatsing van zonlicht.

De volgende wet is geldig voor reflectie: hoekeninval en reflectie liggen in hetzelfde vlak samen met de loodlijn op het reflecterende oppervlak en zijn gelijk aan elkaar.
Breking van licht
Het effect van breking is vergelijkbaar met reflectie, alleen treedt het op als het obstakel in het pad van de lichtstraal een ander transparant medium is. In dit geval wordt een deel van de initiële bundel vanaf het oppervlak gereflecteerd en gaat een deel in het tweede medium. Dit laatste deel wordt de gebroken bundel genoemd en de hoek die het maakt met de loodlijn op het grensvlak wordt de brekingshoek genoemd. De gebroken bundel ligt in hetzelfde vlak als de gereflecteerde en invallende bundel.
Sterke voorbeelden van breking zijn het breken van een potlood in een glas water of de bedrieglijke diepte van een meer wanneer iemand op de bodem kijkt.

Wiskundig wordt dit fenomeen beschreven met behulp van de wet van Snellius. De bijbehorende formule ziet er als volgt uit:
1 sin (θ1)=n2 sin (θ 2).
Hier worden de invalshoeken en brekingshoeken respectievelijk aangeduid als θ1 en θ2. De hoeveelheden n1, n2 weerspiegelen de lichtsnelheid in elk medium. Ze worden de brekingsindices van de media genoemd. Hoe groter n, hoe langzamer het licht in een bepaald materiaal reist. In water is de lichtsnelheid bijvoorbeeld 25% minder dan in lucht, dus daarvoor is de brekingsindex 1,33 (voor lucht is dit 1).
Het fenomeen van totale interne reflectie
De wet van breking van licht leidt tot ééneen interessant resultaat wanneer de straal zich voortplant vanuit een medium met grote n. Laten we in meer detail bekijken wat er in dit geval met de balk zal gebeuren. Laten we de formule van Snell opschrijven:
1 sin (θ1)=n2 sin (θ 2).
We gaan ervan uit dat n1>n2. In dit geval, om de gelijkheid waar te houden, moet θ1 kleiner zijn dan θ2. Deze conclusie is altijd geldig, omdat alleen hoeken van 0o tot 90o worden beschouwd, waarbinnen de sinusfunctie voortdurend toeneemt. Wanneer dus een dichter optisch medium wordt overgelaten aan een minder dicht medium (n1>n2), wijkt de bundel meer af van de normale.
Laten we nu de hoek vergroten θ1. Als resultaat zal het moment komen waarop θ2 gelijk zal zijn aan 90o. Er doet zich een verbazingwekkend fenomeen voor: een bundel die wordt uitgezonden door een dichter medium blijft erin, dat wil zeggen dat het grensvlak tussen twee transparante materialen ondoorzichtig wordt.
Kritische hoek
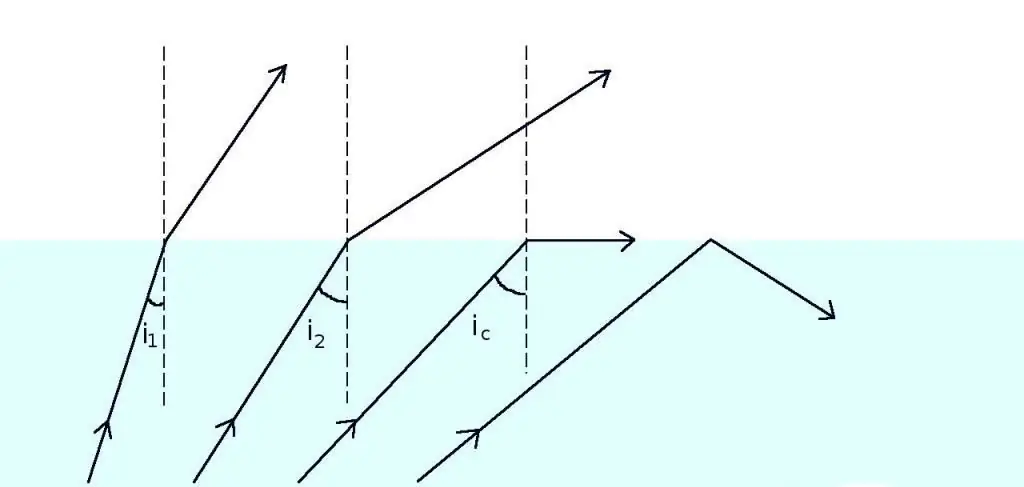
De hoek θ1, waarvoor θ2=90o wordt genoemd cruciaal voor het weloverwogen paar media. Elke straal die het grensvlak raakt onder een hoek die groter is dan de kritische hoek, wordt volledig in het eerste medium gereflecteerd. Voor de kritische hoek θc kan men een uitdrukking schrijven die direct volgt uit de formule van Snell:
sin (θc)=n2 / n1.
Alshet tweede medium is lucht, dan wordt deze gelijkheid vereenvoudigd tot de vorm:
sin (θc)=1 / n1.
De kritische hoek voor water is bijvoorbeeld:
θc=arcsin (1 / 1, 33)=48, 75o.
Als je naar de bodem van het zwembad duikt en omhoog kijkt, kun je de lucht en de wolken er alleen boven je eigen hoofd overheen zien rennen, op de rest van het wateroppervlak zijn alleen de wanden van het zwembad zichtbaar.
Uit de bovenstaande redenering is het duidelijk dat, in tegenstelling tot breking, totale reflectie geen omkeerbaar fenomeen is, het treedt alleen op bij overgang van een dichter naar een minder dicht medium, maar niet omgekeerd.
Totale reflectie in natuur en technologie
Misschien is het meest voorkomende effect in de natuur, dat onmogelijk is zonder totale reflectie, de regenboog. De kleuren van de regenboog zijn het resultaat van de verspreiding van wit licht in regendruppels. Wanneer de stralen echter binnen deze druppels vallen, ervaren ze een enkele of dubbele interne reflectie. Daarom lijkt de regenboog altijd dubbel.
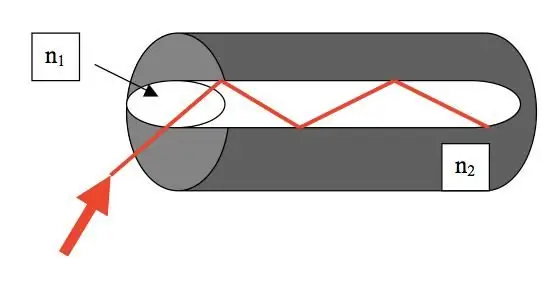
Het fenomeen van interne totale reflectie wordt gebruikt in glasvezeltechnologie. Dankzij optische vezels is het mogelijk om elektromagnetische golven zonder verlies over lange afstanden uit te zenden.






