Iedereen komt tijdens zijn leven lichamen tegen die zich in een van de drie geaggregeerde toestanden van materie bevinden. De eenvoudigste staat van aggregatie om te bestuderen is gas. In het artikel zullen we het concept van een ideaal gas beschouwen, de toestandsvergelijking van het systeem geven en ook enige aandacht besteden aan de beschrijving van de absolute temperatuur.
Gastoestand
Elke student heeft een goed idee van de staat van de materie waar ze het over hebben als ze het woord "gas" horen. Dit woord wordt opgevat als een lichaam dat elk volume kan innemen dat eraan wordt verstrekt. Het is niet in staat om zijn vorm te behouden, omdat het zelfs de geringste invloeden van buitenaf niet kan weerstaan. Ook houdt gas geen volume vast, wat het niet alleen onderscheidt van vaste stoffen, maar ook van vloeistoffen.
Net als een vloeistof is een gas een vloeibare substantie. In het bewegingsproces van vaste lichamen in gassen belemmeren deze laatste deze beweging. De resulterende kracht wordt weerstand genoemd. De waarde ervan hangt af van:snelheid van het lichaam in het gas.
Sterke voorbeelden van gassen zijn lucht, aardgas dat wordt gebruikt voor het verwarmen van huizen en koken, inerte gassen (Ne, Ar) die worden gebruikt om reclamegloeibuizen te vullen of om een inerte (niet-agressieve, beschermende) omgeving te creëren tijdens het lassen.
Ideaal gas
Alvorens verder te gaan met de beschrijving van gaswetten en de toestandsvergelijking, moet u de vraag goed begrijpen wat een ideaal gas is. Dit concept wordt geïntroduceerd in de moleculaire kinetische theorie (MKT). Een ideaal gas is elk gas dat aan de volgende kenmerken voldoet:
- De deeltjes waaruit het bestaat, hebben geen interactie met elkaar, behalve bij directe mechanische botsingen.
- Als gevolg van de botsing van deeltjes met de wanden van het vat of onderling, blijven hun kinetische energie en momentum behouden, dat wil zeggen dat de botsing als absoluut elastisch wordt beschouwd.
- Deeltjes hebben geen afmetingen, maar hebben een eindige massa, dat wil zeggen, ze lijken op materiële punten.
Het is normaal dat elk gas niet ideaal is, maar echt. Niettemin zijn deze benaderingen voor het oplossen van veel praktische problemen redelijk geldig en kunnen ze worden gebruikt. Er is een algemene empirische regel die zegt: ongeacht de chemische aard, als een gas een temperatuur boven kamertemperatuur heeft en een druk in de orde van atmosferische of lager, dan kan het met hoge nauwkeurigheid als ideaal worden beschouwd en kan het worden gebruikt om te beschrijven het.formule van de ideale gastoestandsvergelijking.
Wet Clapeyron-Mendelejev
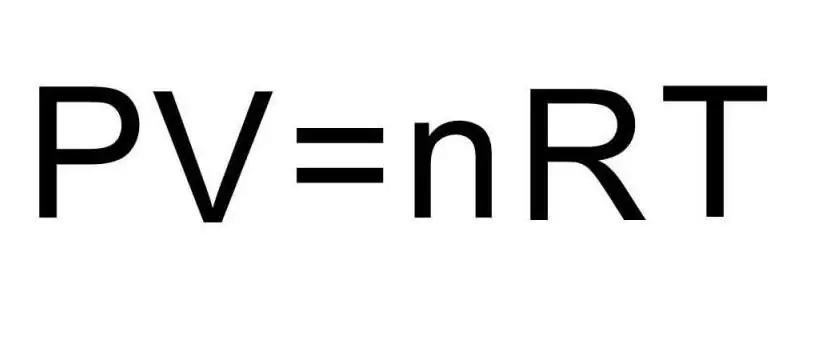
Overgangen tussen verschillende geaggregeerde toestanden van materie en processen binnen een enkele geaggregeerde toestand worden afgehandeld door thermodynamica. Druk, temperatuur en volume zijn drie grootheden die op unieke wijze elke toestand van een thermodynamisch systeem definiëren. De formule voor de toestandsvergelijking van een ideaal gas combineert alle drie deze grootheden tot een enkele gelijkheid. Laten we deze formule schrijven:
PV=nRT
Hier P, V, T - respectievelijk druk, volume, temperatuur. De waarde van n is de hoeveelheid stof in mol, en het symbool R geeft de universele constante van gassen aan. Deze gelijkheid laat zien dat hoe groter het product van druk en volume, hoe groter het product van de hoeveelheid stof en temperatuur moet zijn.

De formule voor de toestandsvergelijking van een gas wordt de wet van Clapeyron-Mendelejev genoemd. In 1834 kwam de Franse wetenschapper Emile Clapeyron, die de experimentele resultaten van zijn voorgangers samenvatte, tot deze vergelijking. Clapeyron gebruikte echter een aantal constanten, die Mendelejev later verving door één - de universele gasconstante R (8, 314 J / (molK)). Daarom is deze vergelijking in de moderne natuurkunde vernoemd naar de namen van Franse en Russische wetenschappers.

Andere vergelijkingsvormen
Hierboven schreven we de Mendelejev-Clapeyron toestandsvergelijking voor een ideaal gas in de algemeen aanvaarde enhandig formulier. Bij problemen in de thermodynamica kan echter vaak een iets andere vorm nodig zijn. Hieronder staan nog drie formules, die direct volgen uit de geschreven vergelijking:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Deze drie vergelijkingen zijn ook universeel voor een ideaal gas, alleen daarin verschijnen hoeveelheden als massa m, molaire massa M, dichtheid ρ en het aantal deeltjes N waaruit het systeem bestaat. Het symbool kB geeft hier de Boltzmann-constante aan (1, 3810-23J/K).
Wet Boyle-Mariotte
Toen Clapeyron zijn vergelijking opstelde, was hij gebaseerd op gaswetten die tientallen jaren eerder experimenteel waren ontdekt. Een daarvan is de wet van Boyle-Mariotte. Het weerspiegelt een isotherm proces in een gesloten systeem, waardoor macroscopische parameters als druk en volume veranderen. Als we T en n constant zetten in de toestandsvergelijking voor een ideaal gas, dan zal de gaswet de vorm aannemen:
P1V1=P2V 2
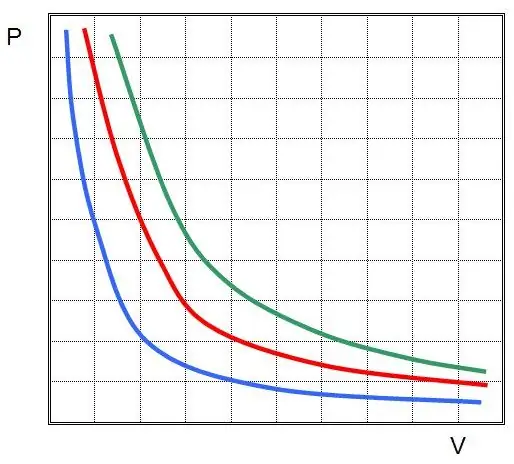
Dit is de wet van Boyle-Mariotte, die zegt dat het product van druk en volume behouden blijft tijdens een willekeurig isotherm proces. In dit geval veranderen de waarden P en V zelf.
Als je P(V) of V(P) plot, dan zijn de isothermen hyperbolen.
Wetten van Charles en Gay-Lussac
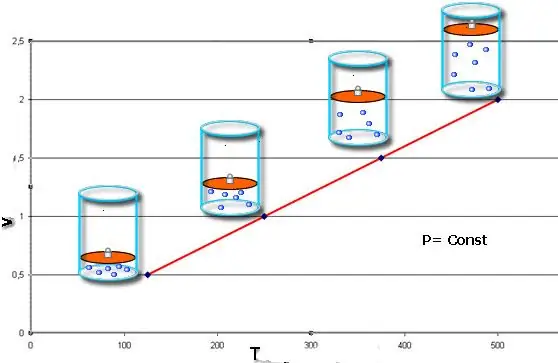
Deze wetten beschrijven wiskundig isobaar en isochoorprocessen, dat wil zeggen dergelijke overgangen tussen de toestanden van het gassysteem, waarin respectievelijk druk en volume behouden blijven. De wet van Charles kan wiskundig als volgt worden geschreven:
V/T=const wanneer n, P=const.
De wet van Gay-Lussac is als volgt geschreven:
P/T=const wanneer n, V=const.
Als beide gelijkheden in de vorm van een grafiek worden weergegeven, krijgen we rechte lijnen die onder een bepaalde hoek met de x-as hellen. Dit type grafiek geeft een directe evenredigheid aan tussen volume en temperatuur bij constante druk en tussen druk en temperatuur bij constant volume.
Merk op dat alle drie de gaswetten geen rekening houden met de chemische samenstelling van het gas, en ook niet met de verandering in de hoeveelheid materie.
Absolute temperatuur
In het dagelijks leven zijn we gewend om de temperatuurschaal van Celsius te gebruiken, omdat het handig is om de processen om ons heen te beschrijven. Dus water kookt bij 100 oC en bevriest bij 0 oC. In de natuurkunde blijkt deze schaal onhandig te zijn, daarom wordt de zogenaamde absolute temperatuurschaal gebruikt, die in het midden van de 19e eeuw door Lord Kelvin werd geïntroduceerd. Volgens deze schaal wordt de temperatuur gemeten in Kelvin (K).
Er wordt aangenomen dat er bij een temperatuur van -273, 15 oC geen thermische trillingen van atomen en moleculen zijn, hun voorwaartse beweging stopt volledig. Deze temperatuur in graden Celsius komt overeen met het absolute nulpunt in Kelvin (0 K). Van deze definitiede fysieke betekenis van absolute temperatuur volgt: het is een maat voor de kinetische energie van de deeltjes waaruit materie bestaat, bijvoorbeeld atomen of moleculen.
Naast de bovenstaande fysieke betekenis van absolute temperatuur, zijn er andere benaderingen om deze hoeveelheid te begrijpen. Een daarvan is de genoemde gaswet van Charles. Laten we het in de volgende vorm schrijven:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
De laatste gelijkheid zegt dat bij een bepaalde hoeveelheid stof in het systeem (bijvoorbeeld 1 mol) en een bepaalde druk (bijvoorbeeld 1 Pa), het gasvolume op unieke wijze de absolute temperatuur bepa alt. Met andere woorden, een toename van het gasvolume onder deze omstandigheden is alleen mogelijk door een toename van de temperatuur, en een afname van het volume duidt op een afname van de waarde van T.
Bedenk dat, in tegenstelling tot Celsius-temperatuur, de absolute temperatuur niet negatief kan zijn.
Avogadro-principe en gasmengsels
Naast de bovenstaande gaswetten leidt de toestandsvergelijking voor een ideaal gas ook tot het principe dat aan het begin van de 19e eeuw door Amedeo Avogadro werd ontdekt en dat zijn achternaam draagt. Dit principe stelt vast dat het volume van elk gas bij constante druk en temperatuur wordt bepaald door de hoeveelheid stof in het systeem. De bijbehorende formule ziet er als volgt uit:
n/V=const wanneer P, T=const.
De geschreven uitdrukking leidt tot de in de ideale gasfysica bekende wet van D alton voor gasmengsels. Dezede wet stelt dat de partiële druk van een gas in een mengsel op unieke wijze wordt bepaald door zijn atoomfractie.
Voorbeeld van probleemoplossing
In een gesloten vat met stijve wanden die een ideaal gas bevatten, nam als gevolg van verwarming de druk met 3 keer toe. Het is noodzakelijk om de eindtemperatuur van het systeem te bepalen als de initiële waarde 25 oC.
was.
Laten we eerst de temperatuur omrekenen van graden Celsius naar Kelvin, we hebben:
T=25 + 273, 15=298, 15 K.
Omdat de wanden van het vat stijf zijn, kan het verwarmingsproces als isochoor worden beschouwd. Voor dit geval passen we de wet van Gay-Lussac toe, we hebben:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
De eindtemperatuur wordt dus bepaald uit het product van de drukverhouding en de begintemperatuur. Als we de gegevens vervangen door gelijkheid, krijgen we het antwoord: T2=894,45 K. Deze temperatuur komt overeen met 621,3 oC.






