Ieder schoolkind weet dat licht in een homogeen transparant medium langs een recht pad beweegt. Dit feit stelt ons in staat om veel optische fenomenen te beschouwen in het kader van het concept van een lichtstraal. Dit artikel gaat over de invalshoek van de straal en waarom het belangrijk is om deze hoek te kennen.
Een lichtstraal is een micrometer elektromagnetische golf
In de natuurkunde zijn er golven van verschillende aard: geluid, zee, elektromagnetisch en enkele andere. De term "bundel" is echter alleen van toepassing op elektromagnetische golven, waarvan het zichtbare spectrum een onderdeel is. Het woord "straal" zelf kan worden weergegeven als een rechte lijn die twee punten in de ruimte verbindt.
Licht (als een golf) kan worden gezien als een rechte lijn, omdat elke golf de aanwezigheid van trillingen impliceert. Het antwoord op deze vraag ligt in de waarde van de golflengte. Dus voor zee en geluid varieert de lengte van enkele centimeters tot tientallen meters. Dergelijke trillingen kunnen natuurlijk moeilijk een straal worden genoemd. De golflengte van licht is minder dan een micrometer. Het menselijk oog is niet in staat om dergelijke trillingen te onderscheiden, daarom lijkt het ons dat:dat we een directe straal zien.
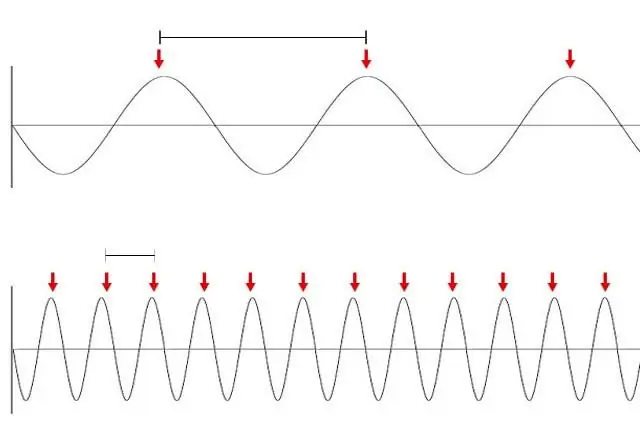
Voor de volledigheid moet worden opgemerkt dat de lichtstraal alleen zichtbaar is wanneer deze begint te verstrooien op kleine deeltjes, zoals in een stoffige ruimte of mistdruppels.
Waar is het belangrijk om de hoek te weten waaronder de straal het obstakel raakt?
De verschijnselen van reflectie en breking zijn de meest bekende optische effecten die een persoon letterlijk elke dag tegenkomt wanneer hij naar zichzelf in de spiegel kijkt of een glas thee drinkt nadat hij naar de lepel erin heeft gekeken.
De wiskundige beschrijving van breking en reflectie vereist kennis van de invalshoek van de bundel. Het fenomeen reflectie wordt bijvoorbeeld gekenmerkt door de gelijkheid van de hoek van reflectie en inval. Indien beschreven vanaf de zijkant van het brekingsproces, zijn de invalshoek en de brekingshoek aan elkaar gerelateerd door de functies van sinussen en de brekingsindices van de media (wet van Snell).

De hoek waaronder een lichtstraal op het grensvlak tussen twee transparante media v alt, speelt een belangrijke rol bij het beschouwen van het effect van interne totale reflectie in een optisch dichter materiaal. Dit effect wordt alleen waargenomen bij invalshoeken die groter zijn dan een bepaalde kritische waarde.
Geometrische definitie van de beschouwde hoek
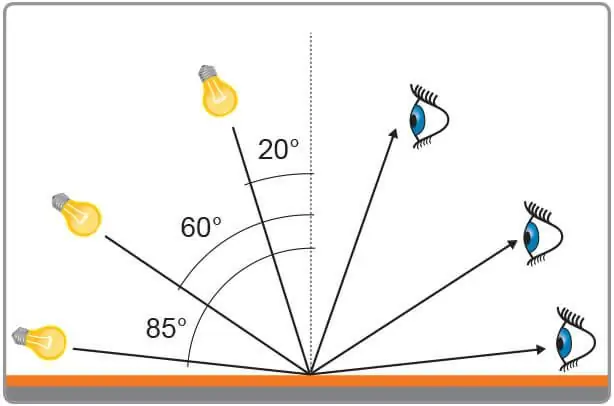
Er kan worden aangenomen dat er een oppervlak is dat de twee omgevingen scheidt. Dit oppervlak kan vlak zijn, zoals in het geval van een spiegel, of het kan complexer zijn, zoals het geribbelde oppervlak van de zee. Stel je voor dat op dit oppervlak v altlichtstraal. Hoe bepaal je de invalshoek van licht? Om dit te doen is vrij eenvoudig. Het volgende is een reeks acties die moeten worden uitgevoerd om de gewenste hoek te vinden.
- Eerst moet je het snijpunt van de straal met het oppervlak bepalen.
- Door O moet men een loodlijn tekenen op het beschouwde oppervlak. Het wordt vaak normaal genoemd.
- De invalshoek van de straal is gelijk aan de hoek tussen de straal en de normaal. Het kan worden gemeten met een eenvoudige gradenboog.
Zoals je kunt zien, is het niet moeilijk om de overwogen hoek te vinden. Studenten maken echter vaak de fout om het tussen het vlak en de balk te meten. Er moet aan worden herinnerd dat de invalshoek altijd wordt gemeten vanaf de normaal, ongeacht de vorm van het oppervlak en het medium waarin het zich voortplant.
Sferische spiegels, lenzen en stralen die erop vallen
Kennis van de eigenschappen van de invalshoeken van bepaalde stralen wordt gebruikt bij de constructie van afbeeldingen in sferische spiegels en dunne lenzen. Om dergelijke afbeeldingen te maken, is het voldoende om te weten hoe twee verschillende bundels zich gedragen bij interactie met de genoemde optische apparaten. Het snijpunt van deze stralen bepa alt de positie van het beeldpunt. In het algemeen zijn er altijd drie verschillende bundels te vinden waarvan het verloop exact bekend is (de derde bundel kan worden gebruikt om de juistheid van het geconstrueerde beeld te controleren). Deze stralen worden hieronder genoemd.
- Loopt parallel aan de optische hoofdas van het apparaat. Het gaat door de focus na reflectie of breking.
- Een straal die door de focus van het apparaat gaat. Het weerspiegelt altijdgebroken evenwijdig aan de hoofdas.
- Door het optische centrum gaan (voor een bolvormige spiegel v alt het samen met het middelpunt van de bol, voor een lens is het erin). Zo'n straal verandert zijn baan niet.
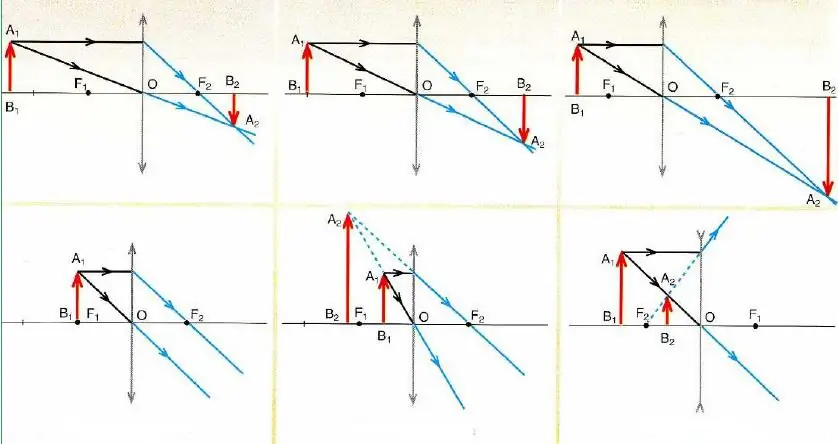
De bovenstaande afbeelding toont de schema's voor het construeren van afbeeldingen voor verschillende opties voor de locatie van het object ten opzichte van dunne lenzen.






