Resolutie is het vermogen van een beeldvormingssysteem om de details van een object te reproduceren, en is afhankelijk van factoren zoals het type verlichting dat wordt gebruikt, de pixelgrootte van de sensor en de mogelijkheden van de optica. Hoe kleiner het detail van het onderwerp, hoe hoger de vereiste resolutie van de lens.
Inleiding tot het oplossingsproces
De beeldkwaliteit van de camera is afhankelijk van de sensor. Simpel gezegd, een digitale beeldsensor is een chip in een camerabody die miljoenen lichtgevoelige plekken bevat. De grootte van de sensor van een camera bepa alt hoeveel licht er kan worden gebruikt om een afbeelding te maken. Hoe groter de sensor, hoe beter de beeldkwaliteit naarmate er meer informatie wordt verzameld. Digitale camera's adverteren doorgaans op de markt voor sensorformaten van 16 mm, Super 35 mm en soms tot 65 mm.
Naarmate de sensor groter wordt, neemt de scherptediepte af bij een bepaald diafragma, omdat je voor een grotere tegenhanger dichterbij moet komenobject of gebruik een langere brandpuntsafstand om het frame te vullen. Om dezelfde scherptediepte te behouden, moet de fotograaf kleinere diafragmaopeningen gebruiken.
Deze geringe scherptediepte kan wenselijk zijn, vooral om achtergrondonscherpte voor portretten te bereiken, maar landschapsfotografie vereist meer diepte, wat gemakkelijker vast te leggen is met het flexibele diafragma van compactcamera's.
Het delen van het aantal horizontale of verticale pixels op een sensor geeft aan hoeveel ruimte elk op een object inneemt, en kan worden gebruikt om het oplossend vermogen van de lens te evalueren en de zorgen van klanten over de pixelgrootte van het digitale beeld van het apparaat op te lossen. Om te beginnen is het belangrijk om te begrijpen wat de resolutie van het systeem daadwerkelijk kan beperken.
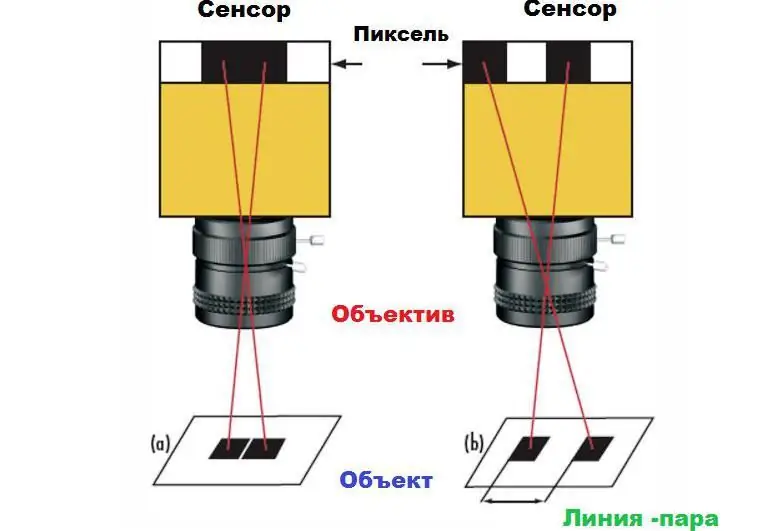
Deze uitspraak kan worden aangetoond door het voorbeeld van een paar vierkanten op een witte achtergrond. Als de vierkanten op de camerasensor worden toegewezen aan aangrenzende pixels, verschijnen ze als één grote rechthoek in de afbeelding (1a) in plaats van twee afzonderlijke vierkanten (1b). Om de vierkanten te onderscheiden, is er een bepaalde ruimte tussen nodig, minimaal één pixel. Deze minimale afstand is de maximale resolutie van het systeem. De absolute limiet wordt bepaald door de grootte van de pixels op de sensor, evenals hun aantal.
Lenskenmerken meten
De relatie tussen afwisselende zwarte en witte vierkanten wordt beschreven als een lineair paar. Meestal wordt de resolutie bepaald door de frequentie,gemeten in lijnparen per millimeter - lp/mm. Lensresolutie in cm is helaas geen absoluut getal. Bij een bepaalde resolutie hangt het vermogen om de twee vierkanten als afzonderlijke objecten te zien af van het grijsschaalniveau. Hoe groter de grijsschaalscheiding tussen hen en de ruimte, des te stabieler is het vermogen om deze vierkanten op te lossen. Deze verdeling van de grijsschaal staat bekend als frequentiecontrast.
Ruimtelijke frequentie wordt gegeven in lp/mm. Om deze reden is het berekenen van de resolutie in termen van lp/mm uitermate handig bij het vergelijken van lenzen en het bepalen van de beste keuze voor bepaalde sensoren en toepassingen. De eerste is waar de berekening van de systeemresolutie begint. Beginnend met de sensor, is het gemakkelijker om te bepalen welke lensspecificaties nodig zijn om te voldoen aan de vereisten van het apparaat of andere toepassingen. De hoogste frequentie toegestaan door de sensor, Nyquist, is in feite twee pixels of één lijnpaar.
Definitie lensresolutie, ook wel systeembeeldruimteresolutie genoemd, kan worden bepaald door de grootte in m te vermenigvuldigen met 2 om een paar te creëren en te delen door 1000 om te converteren naar mm:
lp/mm=1000/ (2 X pixel)
Sensoren met grotere pixels hebben lagere resolutielimieten. Sensoren met kleinere pixels presteren beter volgens de bovenstaande formule voor lensresolutie.
Actief sensorgebied
U kunt de maximale resolutie voor het object berekenenbekijken. Hiervoor is het nodig onderscheid te maken tussen indicatoren zoals de verhouding tussen de grootte van de sensor, het gezichtsveld en het aantal pixels op de sensor. De grootte van de laatste verwijst naar de parameters van het actieve gebied van de camerasensor, meestal bepaald door de grootte van het formaat.
De exacte verhoudingen variëren echter per aspectverhouding, en nominale sensorafmetingen mogen alleen als richtlijn worden gebruikt, vooral voor telecentrische lenzen en hoge vergrotingen. De sensorgrootte kan direct worden berekend uit de pixelgrootte en het actieve aantal pixels om de lensresolutietest uit te voeren.
De tabel toont de Nyquist-limiet die is gekoppeld aan pixelgroottes die te vinden zijn op een aantal veelgebruikte sensoren.
| Pixelgrootte (µm) | Gekoppelde Nyquist-limiet (lp / mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
Naarmate de pixelgrootte afneemt, neemt de bijbehorende Nyquist-limiet in lp/mm evenredig toe. Om de absoluut minimale oplosbare plek te bepalen die op een object te zien is, moet de verhouding van het gezichtsveld tot de grootte van de sensor worden berekend. Dit wordt ook wel primaire augmentatie genoemd.(PMAG) systemen.
De relatie die is gekoppeld aan het systeem PMAG maakt het mogelijk om de resolutie van de beeldruimte te schalen. Bij het ontwerpen van een toepassing wordt deze doorgaans niet gespecificeerd in lp/mm, maar in microns (µm) of fracties van een inch. U kunt snel naar de ultieme resolutie van een object springen door de bovenstaande formule te gebruiken om het kiezen van de lensresolutie z gemakkelijker te maken. Het is ook belangrijk om in gedachten te houden dat er veel aanvullende factoren zijn, en de bovenstaande beperking is veel minder foutgevoelig dan de complexiteit van het in aanmerking nemen van veel factoren en het berekenen ervan met behulp van vergelijkingen.
Bereken de brandpuntsafstand
De resolutie van een afbeelding is het aantal pixels erin. Aangeduid in twee dimensies, bijvoorbeeld 640X480. Er kan voor elke dimensie apart gerekend worden, maar voor de eenvoud wordt dit vaak teruggebracht tot één. Om nauwkeurige metingen op een afbeelding uit te voeren, moet u minimaal twee pixels gebruiken voor elk kleinste gebied dat u wilt detecteren. De grootte van de sensor verwijst naar een fysieke indicator en wordt in de regel niet aangegeven in de paspoortgegevens. De beste manier om de grootte van een sensor te bepalen, is door naar de pixelparameters erop te kijken en deze te vermenigvuldigen met de beeldverhouding, in welk geval het oplossend vermogen van de lens de problemen van een slechte opname oplost.
De Basler acA1300-30um-camera heeft bijvoorbeeld een pixelgrootte van 3,75 x 3,75um en een resolutie van 1296 x 966 pixels. De sensorgrootte is 3,75 µm x 1296 bij 3,75 µm x 966=4,86 x 3,62 mm.
Sensorformaat verwijst naar de fysieke grootte en is niet afhankelijk van de pixelgrootte. Deze instelling wordt gebruikt voor:bepalen met welke lens de camera compatibel is. Om ervoor te zorgen dat ze overeenkomen, moet het lensformaat groter zijn dan of gelijk zijn aan de sensorgrootte. Als een lens met een kleinere beeldverhouding wordt gebruikt, zal het beeld lichtafval ervaren. Hierdoor worden delen van de sensor buiten de rand van het lensformaat donker.
Pixels en cameraselectie

Om de objecten in de afbeelding te zien, moet er voldoende ruimte tussen de objecten zijn zodat ze niet versmelten met aangrenzende pixels, anders zijn ze niet van elkaar te onderscheiden. Als de objecten elk één pixel zijn, moet de scheiding ertussen ook ten minste één element zijn, hierdoor wordt een paar lijnen gevormd, die in feite twee pixels groot zijn. Dit is een van de redenen waarom het onjuist is om de resolutie van camera's en lenzen in megapixels te meten.
Het is eigenlijk gemakkelijker om de resolutiemogelijkheden van een systeem te beschrijven in termen van lijnpaarfrequentie. Hieruit volgt dat naarmate de pixelgrootte afneemt, de resolutie toeneemt, omdat je kleinere objecten op kleinere digitale elementen kunt plaatsen, minder ruimte ertussen kunt hebben en toch de afstand tussen de onderwerpen die je fotografeert kunt oplossen.
Dit is een vereenvoudigd model van hoe de sensor van de camera objecten detecteert zonder rekening te houden met ruis of andere parameters, en is de ideale situatie.
MTF-contrastkaarten
De meeste lenzen zijn geen perfecte optische systemen. Licht dat door een lens gaat, ondergaat een zekere mate van degradatie. De vraag is hoe dit te evaluerendegradatie? Alvorens deze vraag te beantwoorden, is het noodzakelijk om het concept van "modulatie" te definiëren. Deze laatste is een maat voor de contrastlens bij een bepaalde frequentie. Je zou kunnen proberen om afbeeldingen uit de echte wereld die door een lens zijn genomen te analyseren om modulatie of contrast te bepalen voor details van verschillende groottes of frequenties (afstand), maar dit is erg onpraktisch.
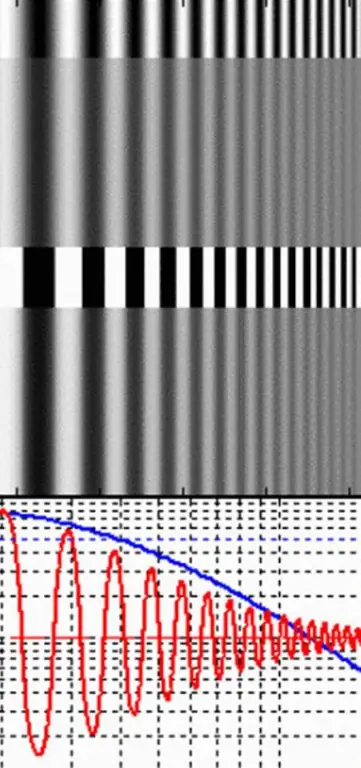
In plaats daarvan is het veel gemakkelijker om modulatie of contrast te meten voor paren afwisselende witte en donkere lijnen. Ze worden rechthoekig rooster genoemd. Het interval van lijnen in een rechthoekig golfrooster is de frequentie (v), waarvoor de modulatie- of contrastfunctie van de lens en de resolutie worden gemeten in cm.
De maximale hoeveelheid licht komt van de lichte banden en de minimale hoeveelheid van de donkere banden. Als licht wordt gemeten in termen van helderheid (L), kan de modulatie worden bepaald volgens de volgende vergelijking:
modulatie=(Lmax - Lmin) / (Lmax + Lmin), waar: Lmax is de maximale helderheid van witte lijnen in het rooster en Lmin is de minimale helderheid van donkere.
Als modulatie wordt gedefinieerd in termen van licht, wordt dit vaak Michelson-contrast genoemd, omdat het de luminantieverhouding van lichte en donkere banden nodig heeft om het contrast te meten.
Er is bijvoorbeeld een blokgolfrooster met een bepaalde frequentie (v) en modulatie, en een inherent contrast tussen donkere en lichte gebieden die door dit rooster door de lens worden gereflecteerd. Beeldmodulatie en dus lenscontrast wordt gemeten voor een bepaalde frequentiematen (v).
De modulatie-overdrachtsfunctie (MTF) wordt gedefinieerd als de modulatie M i van het beeld gedeeld door de modulatie van de stimulus (object) M o, zoals weergegeven in de volgende vergelijking.
|
MTF (v)=M i / M 0 |
USF-testroosters zijn gedrukt op 98% helder laserpapier. Zwarte laserprintertoner heeft een reflectie van ongeveer 10%. Dus de waarde voor M 0 is 88%. Maar aangezien film een beperkter dynamisch bereik heeft in vergelijking met het menselijk oog, is het veilig om aan te nemen dat M 0 in wezen 100% of 1 is. De bovenstaande formule komt dus neer op het volgende meer eenvoudige vergelijking:
|
MTF (v)=Mi |
Dus de MTF-lens voor een gegeven roosterfrequentie (v) is gewoon de gemeten roostermodulatie (Mi) wanneer gefotografeerd door een lens op film.
Microscoop resolutie
De resolutie van een microscoopobjectief is de kortste afstand tussen twee verschillende punten in het gezichtsveld van het oculair die nog steeds als verschillende objecten kunnen worden onderscheiden.
Als twee punten dichter bij elkaar liggen dan je resolutie, zullen ze wazig lijken en zullen hun posities onnauwkeurig zijn. De microscoop kan een hoge vergroting bieden, maar als de lenzen van slechte kwaliteit zijn, zal de resulterende slechte resolutie de beeldkwaliteit verslechteren.
Hieronder staat de Abbe-vergelijking, waarbij de resolutiede kracht van een microscoopobjectief z is het oplossend vermogen gelijk aan de golflengte van het gebruikte licht gedeeld door 2 (de numerieke apertuur van het objectief).
Verschillende elementen beïnvloeden de resolutie van een microscoop. Een optische microscoop die is ingesteld met een hoge vergroting kan een wazig beeld produceren, maar heeft nog steeds de maximale resolutie van de lens.
Het digitale diafragma van een lens is van invloed op de resolutie. Het oplossend vermogen van een microscoopobjectief is een getal dat het vermogen van een lens aangeeft om licht te verzamelen en een punt op een vaste afstand van het objectief op te lossen. Het kleinste punt dat door de lens kan worden opgelost, is evenredig met de golflengte van het verzamelde licht gedeeld door het numerieke apertuurgetal. Daarom komt een groter aantal overeen met een groter vermogen van de lens om een uitstekend punt in het gezichtsveld te detecteren. De numerieke opening van de lens hangt ook af van de hoeveelheid optische aberratiecorrectie.
Resolutie van de telescooplens
Net als een lichttrechter kan een telescoop licht verzamelen in verhouding tot het gebied van het gat, deze eigenschap is de hoofdlens.
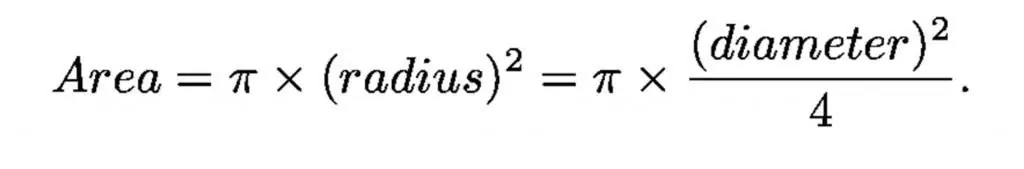
De diameter van de donkere aangepaste pupil van het menselijk oog is iets minder dan 1 centimeter, en de diameter van de grootste optische telescoop is 1000 centimeter (10 meter), zodat de grootste telescoop een miljoen keer groter is in verzameling gebied dan het menselijk oog.

Dit is de reden waarom telescopen zwakkere objecten zien dan mensen. En apparaten hebben die gedurende vele uren licht verzamelen met behulp van elektronische detectiesensoren.
Er zijn twee hoofdtypen telescoop: lensgebaseerde refractors en spiegelgebaseerde reflectoren. Grote telescopen zijn reflectoren omdat spiegels niet transparant hoeven te zijn. Telescoopspiegels behoren tot de meest precieze ontwerpen. De toegestane fout op het oppervlak is ongeveer 1/1000 van de breedte van een mensenhaar - door een gat van 10 meter.
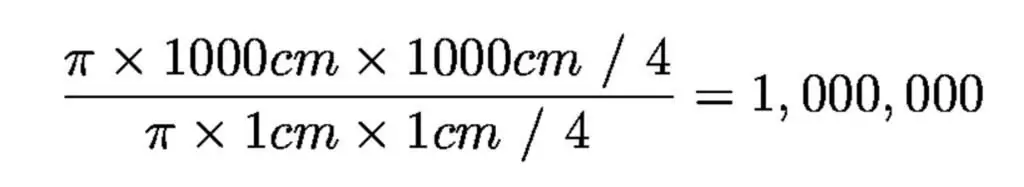
Spiegels werden vroeger gemaakt van enorme dikke glasplaten om te voorkomen dat ze doorbuigen. De spiegels van vandaag zijn dun en flexibel, maar worden computergestuurd of anderszins gesegmenteerd en uitgelijnd door computerbesturing. Naast de taak om vage objecten te vinden, is het doel van de astronoom ook om hun fijne details te zien. De mate waarin details kunnen worden herkend, wordt resolutie genoemd:
- Vage afbeeldingen=slechte resolutie.
- Heldere afbeeldingen=goede resolutie.
Vanwege het golfkarakter van licht en verschijnselen die diffractie worden genoemd, beperkt de diameter van de spiegel of lens van een telescoop de uiteindelijke resolutie ten opzichte van de diameter van de telescoop. De resolutie betekent hier het kleinste hoekdetail dat kan worden herkend. Kleine waarden komen overeen met uitstekende beelddetails.
Radiotelescopen moeten erg groot zijn om een goede resolutie te bieden. De atmosfeer van de aarde isturbulent en wazige telescoopbeelden. Terrestrische astronomen kunnen zelden de maximale resolutie van het apparaat bereiken. Het turbulente effect van de atmosfeer op een ster wordt visie genoemd. Deze turbulentie zorgt ervoor dat de sterren "fonkelen". Om deze atmosferische vervaging te voorkomen, lanceren astronomen telescopen de ruimte in of plaatsen ze op hoge bergen met stabiele atmosferische omstandigheden.
Voorbeelden van parameterberekening
Gegevens om de Canon-lensresolutie te bepalen:
- Pixelgrootte=3,45 µm x 3,45 µm.
- Pixels (H x V)=2448 x 2050.
- Gewenst gezichtsveld (horizontaal)=100 mm.
- Resolutielimiet sensor: 1000/2x3, 45=145 lp / mm.
- Sensorafmetingen: 3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Resolutie meetlens: 145 x 0,0845=12,25 lp/mm.
In feite zijn deze berekeningen behoorlijk ingewikkeld, maar ze zullen je helpen een afbeelding te maken op basis van sensorgrootte, pixelformaat, werkafstand en gezichtsveld in mm. Door deze waarden te berekenen, wordt de beste lens voor uw afbeeldingen en toepassing bepaald.
Problemen van moderne optica

Helaas zorgt een verdubbeling van de sensorgrootte voor extra problemen voor lenzen. Een van de belangrijkste parameters die de kosten van een beeldlens beïnvloeden, is het formaat. Het ontwerpen van een lens voor een groter formaat sensor vereist:talrijke individuele optische componenten, die groter zouden moeten zijn en de overdracht van het systeem stijver.
Een lens die is ontworpen voor een 1"-sensor kan vijf keer zoveel kosten als een lens die is ontworpen voor een ½" -sensor, zelfs als deze niet dezelfde specificaties kan gebruiken met een beperkte pixelresolutie. De kostencomponent moet worden overwogen voordat om het oplossend vermogen van een lens te bepalen.
Optische beeldvorming staat tegenwoordig voor meer uitdagingen dan tien jaar geleden. De sensoren waarmee ze worden gebruikt, hebben veel hogere resolutie-eisen en formaatformaten worden tegelijkertijd zowel kleiner als groter aangedreven, terwijl de pixelgrootte steeds kleiner wordt.
In het verleden beperkte optica het beeldvormingssysteem nooit, tegenwoordig wel. Waar een typische pixelgrootte rond de 9 µm ligt, is een veel gebruikelijkere grootte rond de 3 µm. Deze 81x toename in puntdichtheid heeft zijn tol geëist van de optica, en hoewel de meeste apparaten goed zijn, is lensselectie nu belangrijker dan ooit.






