Basis moleculaire kinetische theorie, vergelijkingen en formules

2024 Auteur: Angel Austin | [email protected]. Laatst gewijzigd: 2023-12-17 05:37

De wereld waarin we leven is onvoorstelbaar mooi en vol met veel verschillende processen die de loop van het leven bepalen. Al deze processen worden bestudeerd door de bekende wetenschap - natuurkunde. Het biedt de mogelijkheid om op zijn minst enig idee te krijgen van de oorsprong van het universum. In dit artikel zullen we een concept beschouwen als moleculaire kinetische theorie, zijn vergelijkingen, typen en formules. Voordat u echter overgaat tot een diepere studie van deze problemen, moet u voor uzelf de betekenis van natuurkunde en de gebieden die het bestudeert, verduidelijken.

Wat is natuurkunde?

In feite is dit een zeer uitgebreide wetenschap en misschien wel een van de meest fundamentele in de geschiedenis van de mensheid. Als dezelfde informatica bijvoorbeeld wordt geassocieerd met bijna elk gebied van menselijke activiteit, of het nu gaat om computationeel ontwerp of het maken van cartoons, dan is natuurkunde het leven zelf, een beschrijving van de complexe processen en stromen. Laten we proberen de betekenis ervan te achterhalen en het begrip zoveel mogelijk te vereenvoudigen.

SoNatuurkunde is dus een wetenschap die zich bezighoudt met de studie van energie en materie, de verbindingen daartussen, de verklaring van vele processen die plaatsvinden in ons enorme universum. De moleculair-kinetische theorie van de structuur van materie is slechts een kleine druppel in de zee van theorieën en takken van de natuurkunde.

Energie, die deze wetenschap in detail bestudeert, kan in verschillende vormen worden weergegeven. Bijvoorbeeld in de vorm van licht, beweging, zwaartekracht, straling, elektriciteit en vele andere vormen. We zullen in dit artikel ingaan op de moleculaire kinetische theorie van de structuur van deze vormen.

De studie van materie geeft ons een idee van de atomaire structuur van materie. Het volgt overigens uit de moleculair-kinetische theorie. De wetenschap van de structuur van materie stelt ons in staat om de betekenis van ons bestaan, de redenen voor het ontstaan van leven en het universum zelf te begrijpen en te vinden. Laten we toch proberen de moleculaire kinetische theorie van materie te bestuderen.

Eerst is enige introductie nodig om de terminologie en eventuele conclusies volledig te begrijpen.

Natuurkundeonderwerpen

Als we de vraag beantwoorden wat moleculair-kinetische theorie is, kan men niet anders dan praten over delen van de natuurkunde. Elk van deze behandelt de gedetailleerde studie en uitleg van een bepaald gebied van het menselijk leven. Ze zijn als volgt ingedeeld:

Mechanica, die is onderverdeeld in nog twee secties: kinematica en dynamiek.
Statisch.
Thermodynamica.
Moleculaire sectie.
Elektrodynamica.
Optica.
Fysica van kwantums en de atoomkern.

Laten we het specifiek hebben over moleculairenatuurkunde, omdat het gebaseerd is op de moleculair-kinetische theorie.

Wat is thermodynamica?

Over het algemeen zijn het moleculaire deel en de thermodynamica nauw verwante takken van de natuurkunde, die uitsluitend de macroscopische component van het totale aantal fysieke systemen bestuderen. Het is de moeite waard eraan te denken dat deze wetenschappen precies de interne toestand van lichamen en stoffen beschrijven. Bijvoorbeeld hun toestand tijdens verwarming, kristallisatie, verdamping en condensatie, op atomair niveau. Met andere woorden, moleculaire fysica is de wetenschap van systemen die bestaan uit een enorm aantal deeltjes: atomen en moleculen.

Het waren deze wetenschappen die de belangrijkste bepalingen van de moleculaire kinetische theorie bestudeerden.

Zelfs in de loop van de zevende klas maakten we kennis met de concepten van micro- en macrowerelden, systemen. Het is niet overbodig om deze termen in het geheugen op te frissen.

De microwereld, zoals we al aan de naam kunnen zien, bestaat uit elementaire deeltjes. Met andere woorden, dit is de wereld van kleine deeltjes. Hun afmetingen worden gemeten in het bereik van 10^-18 m tot 10^-4 m, en de tijd van hun werkelijke toestand kan zowel oneindig als onevenredig kleine intervallen, bijvoorbeeld 10^-20 s.

Macroworld beschouwt lichamen en systemen van stabiele vormen, bestaande uit veel elementaire deeltjes. Dergelijke systemen zijn evenredig met onze menselijke grootte.

Bovendien bestaat er zoiets als een megawereld. Het bestaat uit enorme planeten, kosmische sterrenstelsels en complexen.

Basistheorie

Nu we het een beetje hebben samengevat en de basisvoorwaarden van de natuurkunde hebben onthouden, kunnen we direct naar het hoofdonderwerp van dit artikel gaan.

Moleculair-kinetische theorie verscheen en werd voor het eerst geformuleerd in de negentiende eeuw. De essentie ervan ligt in het feit dat het in detail de structuur van elke stof beschrijft (vaker de structuur van gassen dan vaste en vloeibare lichamen), gebaseerd op drie fundamentele bepalingen die werden verzameld op basis van de veronderstellingen van vooraanstaande wetenschappers als Robert Hooke, Isaac Newton, Daniel Bernoulli, Mikhail Lomonosov en vele anderen.

De belangrijkste bepalingen van de moleculaire kinetische theorie klinken als volgt:

Absoluut alle stoffen (ongeacht of ze vloeibaar, vast of gasvormig zijn) hebben een complexe structuur, bestaande uit kleinere deeltjes: moleculen en atomen. Atomen worden soms "elementaire moleculen" genoemd.
Al deze elementaire deeltjes zijn altijd in een staat van continue en chaotische beweging. Ieder van ons is een direct bewijs van deze stelling tegengekomen, maar hechtte er hoogstwaarschijnlijk niet veel belang aan. Zo zagen we allemaal tegen de achtergrond van de zonnestralen dat stofdeeltjes constant in een chaotische richting bewegen. Dit komt door het feit dat de atomen wederzijdse stoten met elkaar produceren, waardoor ze constant kinetische energie aan elkaar doorgeven. Dit fenomeen werd voor het eerst bestudeerd in 1827, en het werd genoemd naar de ontdekker - "Brownse beweging".
Alle elementaire deeltjes zijn in het proces van continue interactie met elkaar metbepaalde krachten die een elektrische rots hebben.

Het is vermeldenswaard dat een ander voorbeeld dat positie nummer twee beschrijft, dat bijvoorbeeld ook van toepassing kan zijn op de moleculaire kinetische theorie van gassen, diffusie is. We komen het in het dagelijks leven tegen, en in meerdere tests en controles, dus het is belangrijk om er een idee van te hebben.

Beschouw eerst de volgende voorbeelden:

De dokter morste per ongeluk alcohol uit een fles op tafel. Of misschien heb je je parfumflesje laten vallen en verspreidde het zich over de vloer.

Waarom, in deze twee gevallen, zal zowel de geur van alcohol als de geur van parfum na enige tijd de hele kamer vullen, en niet alleen het gebied waar de inhoud van deze stoffen is gemorst?

Het antwoord is simpel: diffusie.

Diffusie - wat is het? Hoe stroomt het?

Dit is een proces waarbij de deeltjes waaruit een bepaalde stof (meestal een gas) bestaat, doordringen in de intermoleculaire holtes van een andere. In onze bovenstaande voorbeelden gebeurde het volgende: door thermische, dat wil zeggen continue en gedissocieerde beweging, vielen alcohol- en/of parfummoleculen in de openingen tussen luchtmoleculen. Geleidelijk, onder invloed van botsingen met atomen en luchtmoleculen, verspreiden ze zich door de kamer. Trouwens, de intensiteit van diffusie, dat wil zeggen de snelheid van zijn stroom, hangt af van de dichtheid van de stoffen die bij diffusie zijn betrokken, evenals van de bewegingsenergie van hun atomen en moleculen, kinetisch genoemd. Hoe groter de kinetische energie, hoe hoger respectievelijk de snelheid van deze moleculen en de intensiteit.

Het snelste diffusieproces kan diffusie in gassen worden genoemd. Dit komt door het feit dat het gas niet homogeen van samenstelling is, wat betekent dat intermoleculaire holtes in gassen respectievelijk een aanzienlijke hoeveelheid ruimte innemen, en het proces om atomen en moleculen van een vreemde substantie erin te krijgen, verloopt gemakkelijker en sneller.

Dit proces is iets langzamer in vloeistoffen. Het oplossen van suikerklontjes in een mok thee is slechts een voorbeeld van de diffusie van een vaste stof in een vloeistof.

Maar de langste tijd is diffusie in lichamen met een vaste kristallijne structuur. Dit is precies zo, omdat de structuur van vaste stoffen homogeen is en een sterk kristalrooster heeft, in de cellen waarvan de atomen van de vaste stof trillen. Als de oppervlakken van twee metalen staven bijvoorbeeld goed worden schoongemaakt en vervolgens met elkaar in contact worden gebracht, kunnen we na een voldoende lange tijd stukjes van het ene metaal in het andere detecteren en vice versa.

Net als elk ander fundamenteel onderdeel, is de basistheorie van de natuurkunde verdeeld in afzonderlijke delen: classificatie, typen, formules, vergelijkingen, enzovoort. Zo hebben we de basis van de moleculaire kinetische theorie geleerd. Dit betekent dat u veilig kunt overgaan tot het overwegen van individuele theoretische blokken.

Moleculair-kinetische theorie van gassen

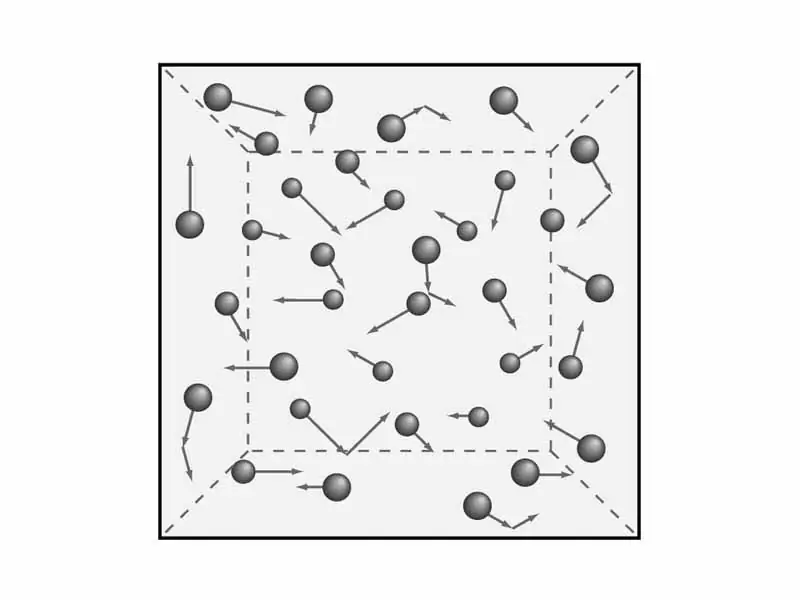
Er is behoefte om de bepalingen van de gastheorie te begrijpen. Zoals we eerder zeiden, zullen we kijken naar de macroscopische eigenschappen van gassen, zoals druk en temperatuur. Dit iszal later nodig zijn om de vergelijking van de moleculair-kinetische gastheorie af te leiden. Maar wiskunde - laten we later, en nu, de theorie en, dienovereenkomstig, natuurkunde behandelen.

Wetenschappers hebben vijf bepalingen van de moleculaire theorie van gassen geformuleerd, die dienen om het kinetische model van gassen te begrijpen. Ze klinken als volgt:

Alle gassen zijn opgebouwd uit elementaire deeltjes die geen bepaalde grootte hebben, maar wel een bepaalde massa. Met andere woorden, het volume van deze deeltjes is minimaal in vergelijking met de lengte ertussen.
Atomen en moleculen van gassen hebben praktisch geen potentiële energie, respectievelijk volgens de wet is alle energie gelijk aan kinetisch.
We maakten al eerder kennis met deze positie - Brownse beweging. Dat wil zeggen, gasdeeltjes zijn altijd in continue en chaotische beweging.
Absoluut alle onderlinge botsingen van gasdeeltjes, vergezeld van de boodschap van snelheid en energie, zijn volledig elastisch. Dit betekent dat er geen energieverlies of scherpe sprongen in hun kinetische energie optreden tijdens een botsing.
Onder normale omstandigheden en constante temperatuur is de gemiddelde energie van deeltjesbeweging van bijna alle gassen hetzelfde.

We kunnen de vijfde positie herschrijven via dit type vergelijking van de moleculair-kinetische gastheorie:

E=1/2mv^2=3/2kT, waarbij k de Boltzmann-constante is; T - temperatuur in Kelvin.

Deze vergelijking geeft ons inzicht in de relatie tussen de snelheid van elementaire gasdeeltjes en hun absolute temperatuur. Dienovereenkomstig, hoe hoger hun absolutetemperatuur, hoe groter hun snelheid en kinetische energie.

Gasdruk

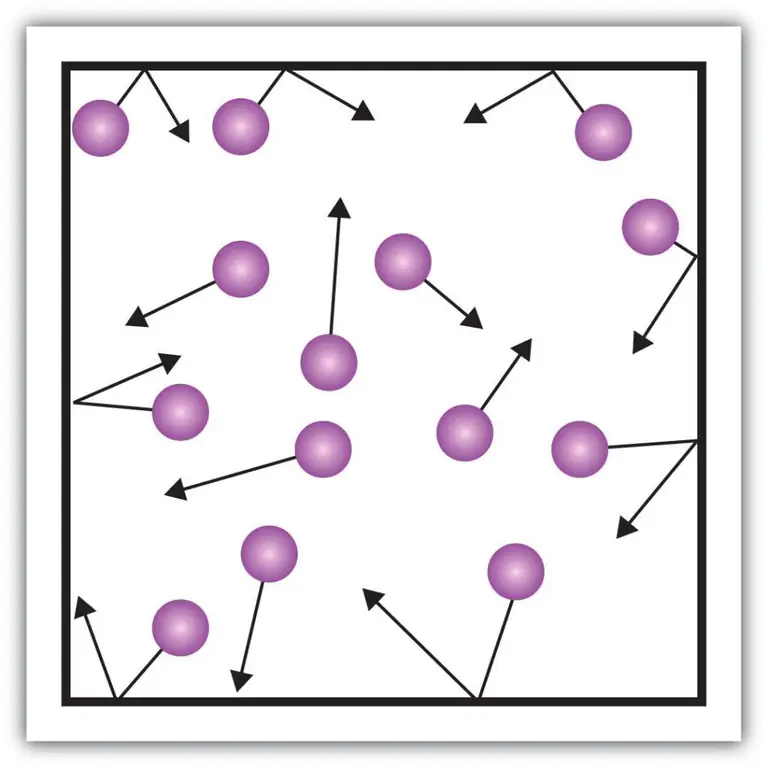
Dergelijke macroscopische componenten van de karakteristiek, zoals de druk van gassen, kunnen ook worden verklaard met behulp van de kinetische theorie. Laten we ons hiervoor het volgende voorbeeld voorstellen.

Laten we aannemen dat een molecuul van een gas zich in een doos bevindt, waarvan de lengte L is. Laten we de bepalingen van de hierboven beschreven gastheorie gebruiken en rekening houden met het feit dat de moleculaire bol alleen langs de x beweegt -as. Zo kunnen we het proces van elastische botsing met een van de wanden van het vat (doos) observeren.

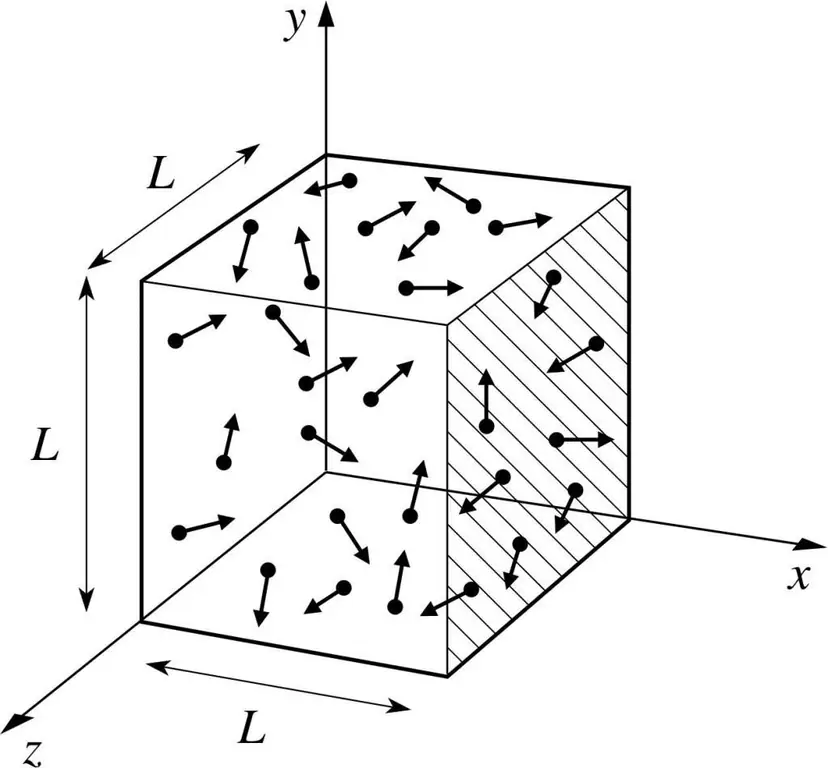
Het momentum van de aanhoudende botsing wordt, zoals we weten, bepaald door de formule: p=mv, maar in dit geval zal deze formule een projectievorm aannemen: p=mv(x).

Aangezien we alleen de dimensie van de x-as beschouwen, dat wil zeggen de x-as, wordt de totale verandering in momentum uitgedrukt door de formule: mv(x) - m(-v(x))=2mv(x).

Beschouw vervolgens de kracht die door ons object wordt uitgeoefend met behulp van de tweede wet van Newton: F=ma=P/t.

Vanuit deze formules drukken we de druk van de gaszijde uit: P=F/a;

Laten we nu de krachtuitdrukking in de resulterende formule vervangen en krijgen: P=mv(x)^2/L^3.

Daarna kan onze voltooide drukformule worden geschreven voor het N-de aantal gasmoleculen. Met andere woorden, het ziet er als volgt uit:

P=Nmv(x)^2/V, waarbij v snelheid is en V volume.

Laten we nu proberen een paar basisbepalingen over gasdruk te benadrukken:

Het manifesteert zich doorbotsingen van moleculen met moleculen van de wanden van het object waarin het zich bevindt.
De grootte van de druk is recht evenredig met de kracht en snelheid van de impact van moleculen op de wanden van het vat.

Enkele korte conclusies over theorie

Voordat we verder gaan en de basisvergelijking van de moleculaire kinetische theorie beschouwen, bieden we u een paar korte conclusies uit de bovenstaande punten en theorie:

De maat voor de gemiddelde bewegingsenergie van zijn atomen en moleculen is de absolute temperatuur.
Als twee verschillende gassen dezelfde temperatuur hebben, hebben hun moleculen dezelfde gemiddelde kinetische energie.
De energie van gasdeeltjes is recht evenredig met de gemiddelde kwadratische snelheid: E=1/2mv^2.
Hoewel gasmoleculen respectievelijk een gemiddelde kinetische energie en een gemiddelde snelheid hebben, bewegen individuele deeltjes met verschillende snelheden: sommige snel, andere langzaam.
Hoe hoger de temperatuur, hoe hoger de snelheid van de moleculen.
Hoe vaak we de temperatuur van het gas verhogen (bijvoorbeeld verdubbelen), de bewegingsenergie van zijn deeltjes neemt even vaak toe (respectievelijk verdubbelt).

Basisvergelijking en formules

Met de basisvergelijking van de moleculaire kinetische theorie kun je de relatie vaststellen tussen de grootheden van de microwereld en, dienovereenkomstig, de macroscopische, dat wil zeggen gemeten, grootheden.

Een van de eenvoudigste modellen die de moleculaire theorie kan overwegen, is het ideale gasmodel.

Dat zou je kunnen zeggendit is een soort denkbeeldig model bestudeerd door de moleculaire kinetische theorie van een ideaal gas, waarin:

de eenvoudigste gasdeeltjes worden beschouwd als perfect elastische ballen die in slechts één geval zowel met elkaar als met de moleculen van de wanden van een vat interageren - een absoluut elastische botsing;
de aantrekkingskrachten in het gas zijn afwezig of kunnen zelfs worden verwaarloosd;
elementen van de interne structuur van het gas kunnen als materiële punten worden beschouwd, dat wil zeggen, hun volume kan ook worden verwaarloosd.

Overwegend een dergelijk model, schreef de in Duitsland geboren natuurkundige Rudolf Clausius een formule voor gasdruk door de relatie van micro- en macroscopische parameters. Het ziet eruit als:

p=1/3m(0)nv^2.

Later zal deze formule worden genoemd als de basisvergelijking van de moleculair-kinetische theorie van een ideaal gas. Het kan in verschillende vormen worden gepresenteerd. Het is nu onze taak om secties te laten zien zoals moleculaire fysica, moleculaire kinetische theorie, en dus hun volledige vergelijkingen en typen. Daarom is het zinvol om andere varianten van de basisformule te overwegen.

We weten dat de gemiddelde energie die de beweging van gasmoleculen kenmerkt, kan worden gevonden met behulp van de formule: E=m(0)v^2/2.

In dit geval kunnen we de uitdrukking m(0)v^2 in de oorspronkelijke drukformule vervangen door de gemiddelde kinetische energie. Als resultaat hiervan zullen we de mogelijkheid hebben om de basisvergelijking van de moleculaire kinetische theorie van gassen op te stellen in de volgende vorm: p=2/3nE.

Bovendien weten we allemaal dat de uitdrukking m(0)n kan worden geschreven als een product van twee quotiënten:

m/NN/V=m/V=ρ.

Na deze manipulaties kunnen we onze formule herschrijven voor de vergelijking van de moleculair-kinetische theorie van een ideaal gas in een derde, andere vorm:

p=1/3ρv^2.

Nou, misschien is dat alles wat je moet weten over dit onderwerp. Het blijft alleen om de opgedane kennis te systematiseren in de vorm van korte (en niet zo) conclusies.

Alle algemene conclusies en formules over het onderwerp "Moleculair-kinetische theorie"

Dus laten we beginnen.

Eerste:

Natuurkunde is een fundamentele wetenschap die deel uitmaakt van de natuurwetenschappen en die de eigenschappen van materie en energie, hun structuur, patronen van anorganische aard bestudeert.

Het bevat de volgende secties:

mechanica (kinematica en dynamiek);
statisch;
thermodynamica;
elektrodynamica;
moleculaire sectie;
optica;
fysica van kwantums en de atoomkern.

Tweede:

Deeltjesfysica en thermodynamica zijn nauw verwante takken die de uitsluitend macroscopische component van het totale aantal fysieke systemen bestuderen, dat wil zeggen systemen die bestaan uit een groot aantal elementaire deeltjes.

Ze zijn gebaseerd op de moleculaire kinetische theorie.

Derde:

De kern van de zaak is dit. De moleculaire kinetische theorie beschrijft in detail de structuur van een stof (vaker de structuur van gassen dan van vaste stoffen).en vloeibare lichamen), gebaseerd op drie fundamentele veronderstellingen die werden verzameld op basis van de veronderstellingen van vooraanstaande wetenschappers. Onder hen: Robert Hooke, Isaac Newton, Daniel Bernoulli, Mikhail Lomonosov en vele anderen.

Vierde:

Drie basisprincipes van de moleculaire kinetische theorie:

Alle stoffen (ongeacht of ze vloeibaar, vast of gasvormig zijn) hebben een complexe structuur die bestaat uit kleinere deeltjes: moleculen en atomen.
Al deze eenvoudige deeltjes zijn in continue chaotische beweging. Voorbeeld: Brownse beweging en diffusie.
Alle moleculen werken onder alle omstandigheden met elkaar in wisselwerking met bepaalde krachten die een elektrische rots hebben.

Elk van deze bepalingen van de moleculaire kinetische theorie vormt een solide basis in de studie van de structuur van materie.

Vijfde:

Verschillende hoofdpunten van de moleculaire theorie voor het gasmodel:

Alle gassen zijn opgebouwd uit elementaire deeltjes die geen bepaalde grootte hebben, maar wel een bepaalde massa. Met andere woorden, het volume van deze deeltjes is minimaal in vergelijking met de afstanden ertussen.
Atomen en moleculen van gassen hebben respectievelijk praktisch geen potentiële energie, hun totale energie is gelijk aan de kinetische.
We maakten al eerder kennis met deze positie - Brownse beweging. Dat wil zeggen, gasdeeltjes zijn altijd in continue en willekeurige beweging.
Absoluut alle onderlinge botsingen van atomen en moleculen van gassen, vergezeld van de boodschap van snelheid en energie, zijn volledig elastisch. Dit isbetekent dat er geen energieverlies of scherpe sprongen in hun kinetische energie zijn tijdens een botsing.
Onder normale omstandigheden en constante temperatuur is de gemiddelde kinetische energie van bijna alle gassen hetzelfde.

Zesde:

Conclusies uit de theorie over gassen:

Absolute temperatuur is een maat voor de gemiddelde kinetische energie van zijn atomen en moleculen.
Als twee verschillende gassen dezelfde temperatuur hebben, hebben hun moleculen dezelfde gemiddelde kinetische energie.
De gemiddelde kinetische energie van gasdeeltjes is recht evenredig met de gemiddelde kwadratische snelheid: E=1/2mv^2.
Hoewel gasmoleculen respectievelijk een gemiddelde kinetische energie en een gemiddelde snelheid hebben, bewegen individuele deeltjes met verschillende snelheden: sommige snel, andere langzaam.
Hoe hoger de temperatuur, hoe hoger de snelheid van de moleculen.
Hoe vaak we de temperatuur van het gas verhogen (bijvoorbeeld verdubbelen), de gemiddelde kinetische energie van zijn deeltjes neemt ook zo vaak toe (respectievelijk verdubbelt).
De relatie tussen de druk van een gas op de wanden van het vat waarin het zich bevindt en de intensiteit van de inslagen van moleculen op deze wanden is recht evenredig: hoe meer inslagen, hoe hoger de druk en vice versa.

Zevende:

Een ideaal gasmodel is een model waarbij aan de volgende voorwaarden moet worden voldaan:

Gasmoleculen kunnen en worden beschouwd als perfect elastische ballen.
Deze ballen kunnen met elkaar communiceren en met de muren van elkeschip in slechts één geval - absoluut elastische aanvaring.
De krachten die de onderlinge stuwkracht tussen atomen en moleculen van een gas beschrijven, zijn afwezig of kunnen zelfs worden verwaarloosd.
Atomen en moleculen worden beschouwd als materiële punten, dat wil zeggen dat hun volume ook kan worden verwaarloosd.

Achtste:

Laten we alle basisvergelijkingen geven en de formules laten zien in het onderwerp "Moleculair-kinetische theorie":

p=1/3m(0)nv^2 - de basisvergelijking voor het ideale gasmodel, afgeleid door de Duitse natuurkundige Rudolf Clausius.

p=2/3nE - de basisvergelijking van de moleculair-kinetische theorie van een ideaal gas. Afgeleid van de gemiddelde kinetische energie van de moleculen.

р=1/3ρv^2 - dezelfde vergelijking, maar beschouwd door de dichtheid en de gemiddelde kwadratische snelheid van ideale gasmoleculen.

m(0)=M/N(a) - de formule voor het vinden van de massa van één molecuul via het Avogadro-getal.

v^2=(v(1)+v(2)+v(3)+…)/N - formule voor het vinden van de gemiddelde kwadratische snelheid van moleculen, waarbij v(1), v(2), v (3) enzovoort - de snelheid van het eerste molecuul, het tweede, het derde enzovoort tot het n-de molecuul.

n=N/V - formule voor het vinden van de concentratie van moleculen, waarbij N het aantal moleculen in een gasvolume is tot een bepaald volume V.

E=mv^2/2=3/2kT - formules voor het vinden van de gemiddelde kinetische energie van moleculen, waarbij v^2 de kwadratische gemiddelde snelheid van moleculen is, k is een constante waarde genoemd naar de Oostenrijker de fysica van Ludwig Boltzmann, en T is de temperatuur van het gas.

p=nkT - drukformule in termen van concentratie, constantBoltzmann en de absolute temperatuur T. Hieruit volgt een andere fundamentele formule, ontdekt door de Russische wetenschapper Mendelejev en de Franse natuurkundige-ingenieur Claiperon:

pV=m/MRT, waarbij R=kN(a) de universele constante voor gassen is.

Laten we nu constanten tonen voor verschillende iso-processen: isobaar, isochoor, isotherm en adiabatisch.

pV/T=const - uitgevoerd wanneer de massa en samenstelling van het gas constant zijn.

рV=const - als de temperatuur ook constant is.

V/T=const - als de gasdruk constant is.

p/T=const - als het volume constant is.

Misschien is dat alles wat u over dit onderwerp moet weten.

Vandaag zijn we ondergedompeld in zo'n wetenschappelijk veld als theoretische natuurkunde, zijn meerdere secties en blokken. In meer detail hebben we een dergelijk gebied van de fysica aangeroerd als fundamentele moleculaire fysica en thermodynamica, namelijk de moleculaire-kinetische theorie, die, naar het lijkt, geen problemen oplevert in de eerste studie, maar in feite veel valkuilen heeft. Het vergroot ons begrip van het ideale gasmodel, dat we ook in detail hebben bestudeerd. Bovendien is het vermeldenswaard dat we ook kennis hebben gemaakt met de basisvergelijkingen van de moleculaire theorie in hun verschillende variaties, en ook de meest noodzakelijke formules hebben overwogen om bepaalde onbekende grootheden over dit onderwerp te vinden. Dit zal vooral handig zijn bij het voorbereiden van het schrijven eventuele tests, examens en tests, of om de algemene kijk en kennis van de natuurkunde uit te breiden.

We hopen dat dit artikel nuttig voor je was, en dat je er alleen de meest noodzakelijke informatie uit hebt gehaald, waardoor je je kennis hebt versterkt in zulke pijlers van de thermodynamica als de basisbepalingen van de moleculaire kinetische theorie.