Bij peer review, bijvoorbeeld om het concurrentievermogen van producten te beoordelen, is het, zoals bij elk wetenschappelijk werk, noodzakelijk om statistische gegevensverwerking uit te voeren. Dit laatste begint met het bepalen van de consistentie van de meningen van deskundigen, waarvan de numerieke uitdrukking de concordantiecoëfficiënt is.
Waarom hebben we een deskundige consensusbeoordeling nodig?
Deze beoordeling is in de eerste plaats noodzakelijk omdat de meningen van experts sterk kunnen verschillen over de geschatte parameters. De beoordeling vindt in eerste instantie plaats door de indicatoren te rangschikken en er een bepaalde significantiecoëfficiënt (gewicht) aan toe te kennen. Een inconsistente rangschikking heeft tot gevolg dat deze coëfficiënten statistisch onbetrouwbaar zijn. De meningen van experts met hun vereiste aantal (meer dan 7-10) moeten worden verspreid volgens de normale wet.
Het concept van de concordantiecoëfficiënt
Dus. Consistentie is overeenstemming. De coëfficiënt is een dimensieloze grootheid die de verhouding van de dispersie tot de maximale dispersie in het algemene geval aangeeft. Laten we deze concepten generaliseren.
Concordantiecoëfficiënt is een getal van 0 tot 1, dat de consistentie van expertmeningen aangeeft wanneerrangschikken van een aantal eigenschappen. Hoe dichter deze waarde bij 0 ligt, hoe lager de consistentie wordt beschouwd. Als de waarde van deze coëfficiënt kleiner is dan 0,3, worden de meningen van experts als inconsistent beschouwd. Wanneer de waarde van de coëfficiënt tussen 0,3 en 0,7 ligt, wordt de consistentie als gemiddeld beschouwd. Een waarde groter dan 0,7 wordt beschouwd als een hoge consistentie.
Gebruiksgevallen
Bij het uitvoeren van statistisch onderzoek kunnen zich situaties voordoen waarin een object niet wordt gekenmerkt door twee reeksen, die statistisch worden verwerkt met behulp van de concordantiecoëfficiënt, maar door meerdere reeksen, die dienovereenkomstig worden gerangschikt door experts met hetzelfde niveau van professionaliteit op een bepaald gebied.
De consistentie van de door experts uitgevoerde rangschikking moet worden bepaald om de juistheid te bevestigen van de hypothese dat experts relatief nauwkeurige metingen doen, waardoor verschillende groepen in expertgroepen kunnen worden gevormd, die grotendeels worden bepaald door menselijke factoren, voornamelijk zoals verschillen in opvattingen, concepten, verschillende wetenschappelijke scholen, de aard van professionele activiteit, enz.
Korte beschrijving van de rangschikkingsmethode. De voor- en nadelen ervan
Bij het rangschikken wordt de rangschikkingsmethode gebruikt. De essentie ligt in het feit dat elke eigenschap van het object zijn eigen specifieke rang krijgt. Bovendien wordt aan elke expert die deel uitmaakt van de expertgroep, deze rang toegekendonafhankelijk, waardoor het nodig is deze gegevens te verwerken om de consistentie van de meningen van deskundigen vast te stellen. Dit proces wordt uitgevoerd door de concordantiecoëfficiënt te berekenen.
Het belangrijkste voordeel van de rangschikkingsmethode is het gemak van implementatie.
De belangrijkste nadelen van de methode zijn:
- een klein aantal rangschikkingsobjecten, aangezien wanneer hun aantal groter is dan 15-20, het moeilijk wordt om objectieve rangschikkingsscores toe te kennen;
- Op basis van het gebruik van deze methode blijft de vraag open hoe ver de bestudeerde objecten in betekenis van elkaar verwijderd zijn.
Bij het gebruik van deze methode moet er rekening mee worden gehouden dat de beoordelingen gebaseerd zijn op een soort probabilistisch model, dus ze moeten met de nodige voorzichtigheid worden toegepast, gezien de reikwijdte.
Kendall's Concordance Rang Coëfficiënt
Wordt gebruikt om de relatie te bepalen tussen kwantitatieve en kwalitatieve kenmerken die homogene objecten kenmerken en gerangschikt volgens hetzelfde principe.
Deze coëfficiënt wordt bepaald door de formule:
t=2S/(n(n-1)), waarbij
S - de som van de verschillen tussen het aantal reeksen en het aantal inversies op het tweede kenmerk;
n - aantal waarnemingen.

Berekeningsalgoritme:
- De x-waarden zijn gerangschikt in oplopende of aflopende volgorde.
- De y-waarden zijn gerangschikt in de volgorde waarin ze overeenkomen met de x-waarden.
- Bepaal voor elke opeenvolgende rangorde van y hoeveel hogere rangwaarden erop volgen. Ze worden opgeteld en de mate van overeenstemming van rijen van rijen in x en y wordt berekend.
- Op dezelfde manier wordt het aantal rangen van y met lagere waarden berekend, die ook optellen.
- Voeg het aantal rangen met hogere waarden en het aantal rangen met lagere waarden toe, wat resulteert in de waarde S.
Deze coëfficiënt toont de relatie tussen twee variabelen en wordt in de meeste gevallen de Kendall-rangcorrelatiecoëfficiënt genoemd. Een dergelijke afhankelijkheid kan grafisch worden weergegeven.
Bepaling van de coëfficiënt
Hoe wordt het gedaan? Als het aantal gerangschikte kenmerken of factoren groter is dan 2, wordt de concordantiecoëfficiënt gebruikt, die in wezen een meervoudige variant van rangcorrelatie is.
Wees voorzichtig. De berekening van de concordantiecoëfficiënt is gebaseerd op de verhouding van de afwijking van de som van de kwadraten van rangen van de gemiddelde som van de kwadraten van rangen, vermenigvuldigd met 12, tot het kwadraat van experts, vermenigvuldigd met het verschil tussen de derde macht van het aantal van objecten en het aantal objecten.
Berekeningsalgoritme
Om te begrijpen waar het getal 12 vandaan komt in de teller van de berekeningsformule, laten we eens kijken naar het bepalingsalgoritme.
Voor elke regel met de rangen van een bepaalde expert wordt de som van de rangen berekend, wat een willekeurige waarde is.
De concordantiecoëfficiënt wordt over het algemeen gedefinieerd als de verhouding van de variantieschatting (D) tot de maximale waarde van de variantieschatting(Dmax). Laten we achtereenvolgens de definities van deze grootheden formuleren.
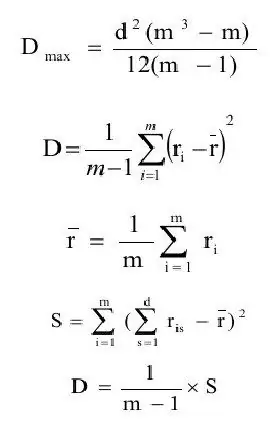
waar ravg - schatting van de verwachting;
m - aantal objecten.
Door de resulterende formules in relatie tot D te vervangen door Dmax krijgen we de uiteindelijke formule voor de concordantiecoëfficiënt:
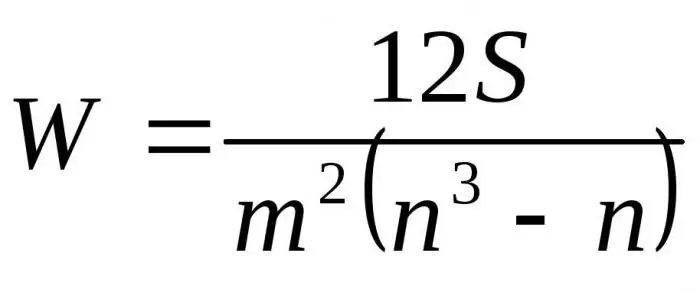
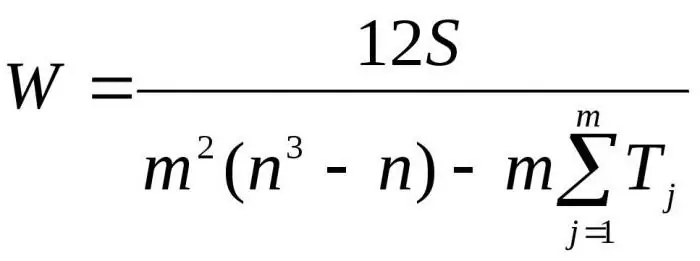
Hier is m het aantal experts, n is het aantal objecten.
De eerste formule wordt gebruikt om de concordantiefactor te bepalen als er geen gerelateerde rangen zijn. De tweede formule wordt gebruikt als er gerelateerde rangen zijn.
Dus, de berekening van de concordantiecoëfficiënt is voorbij. Wat is het volgende? De verkregen waarde wordt geëvalueerd op significantie met behulp van de Pearson-coëfficiënt door deze coëfficiënt te vermenigvuldigen met het aantal experts en met het aantal vrijheidsgraden (m-1). Het resulterende criterium wordt vergeleken met de tabelwaarde, en als de waarde van de eerste de laatste overschrijdt, spreken ze van de significantie van de bestudeerde coëfficiënt.
In het geval van gerelateerde rangen wordt de berekening van het Pearson-criterium iets gecompliceerder en wordt uitgevoerd met de volgende verhouding: (12S)/(d(m2+) m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Voorbeeld
Veronderstel dat de expertmethode het concurrentievermogen evalueert van boter die in een retailnetwerk wordt verkocht. Laten we een voorbeeld geven van het berekenen van de concordantiecoëfficiënt. Alvorens het concurrentievermogen te beoordelen, is het noodzakelijk om de consument te rangschikkeneigenschappen van dit product die bij de beoordeling betrokken zijn. Laten we aannemen dat deze eigenschappen de volgende zijn: smaak en geur, consistentie en uiterlijk, kleur, verpakking en etikettering, vetgeh alte, handelsnaam, fabrikant, prijs.
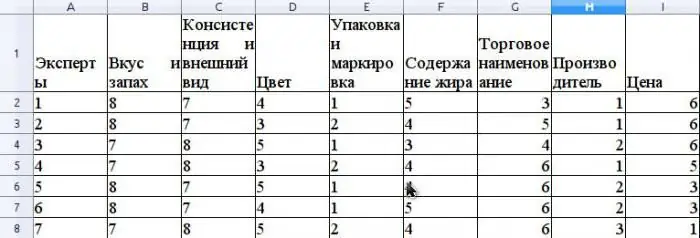
Veronderstel dat de expertgroep uit 7 experts bestaat. De afbeelding toont de resultaten van het rangschikken van deze eigenschappen.
De gemiddelde waarde van r wordt berekend als het rekenkundig gemiddelde en is 31,5. Om S te vinden, tel de gekwadrateerde verschillen tussen ris en r-gemiddelde op, volgens de formule hierboven, en bepaal dat de waarde van S 1718 is.
Bereken de concordantiecoëfficiënt met behulp van de formule zonder gerelateerde rangen te gebruiken (rangen zouden gerelateerd zijn als dezelfde Expert Advisor dezelfde rangen had voor verschillende eigenschappen).
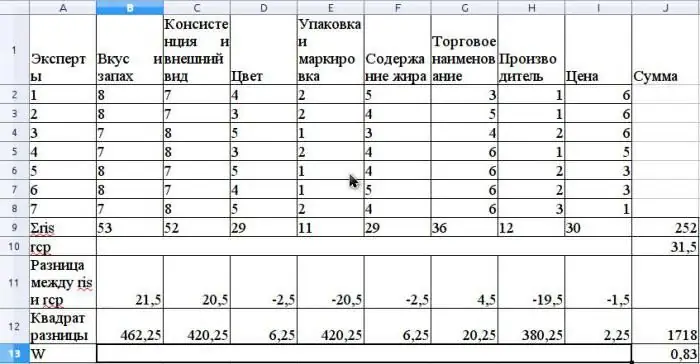
De waarde van deze coëfficiënt is 0,83. Dit duidt op een sterke consensus onder experts.
Controleer de betekenis ervan met de Pearson-test:
7 x 0,83 x (8-1)=40,7.
Pearson's test in tabelvorm bij een significantieniveau van 1% is 18,5 en bij 5% - 14,1..
Het voorbeeld demonstreert de eenvoud en toegankelijkheid van de berekening voor iedereen die de basis van wiskundige berekeningen kent. Om ze te verlichten,gebruik spreadsheetformulieren.
Tot slot
De concordantiecoëfficiënt toont dus de consistentie van de meningen van verschillende experts. Hoe verder van 0 en dichter bij 1, hoe consistenter de meningen. Deze coëfficiënten moeten worden bevestigd door het Pearson-criterium te berekenen.






