Elasticiteitsmodulus is een fysieke grootheid die het elastische gedrag van een materiaal kenmerkt wanneer er een externe kracht op wordt uitgeoefend in een bepaalde richting. Het elastische gedrag van een materiaal betekent zijn vervorming in het elastische gebied.
Geschiedenis van de studie van elasticiteit van materialen

De natuurkundige theorie van elastische lichamen en hun gedrag onder invloed van externe krachten werd in detail beschouwd en bestudeerd door de Engelse wetenschapper van de 19e eeuw, Thomas Young. Het begrip elasticiteit zelf werd echter al in 1727 ontwikkeld door de Zwitserse wiskundige, natuurkundige en filosoof Leonhard Euler, en de eerste experimenten met betrekking tot de elasticiteitsmodulus werden uitgevoerd in 1782, dat wil zeggen 25 jaar vóór het werk van Thomas Jung, door de Venetiaanse wiskundige en filosoof Jacopo Ricatti.
De verdienste van Thomas Young ligt in het feit dat hij de elasticiteitstheorie een slank, modern uiterlijk gaf, dat vervolgens werd geformaliseerd in de vorm van een eenvoudige en vervolgens algemene wet van Hooke.
Fysieke aard van elasticiteit
Elk lichaam bestaat uit atomen, waartussen de krachten van aantrekking en afstoting werken. De balans van deze krachten isde toestand en parameters van materie onder bepaalde omstandigheden. De atomen van een vast lichaam beginnen, wanneer er onbeduidende externe krachten van spanning of compressie op worden uitgeoefend, te verschuiven, waardoor een tegengestelde richting en even grote kracht ontstaat, die de atomen terugbrengt naar hun oorspronkelijke staat.
Tijdens het proces van een dergelijke verplaatsing van atomen neemt de energie van het hele systeem toe. Experimenten tonen aan dat bij kleine rekjes de energie evenredig is met het kwadraat van deze rekjes. Dit betekent dat de kracht, die een afgeleide is van energie, evenredig blijkt te zijn met de eerste macht van de rek, dat wil zeggen dat deze er lineair van afhangt. Als we de vraag beantwoorden wat de elasticiteitsmodulus is, kunnen we zeggen dat dit de evenredigheidscoëfficiënt is tussen de kracht die op het atoom inwerkt en de vervorming die deze kracht veroorzaakt. De dimensie van Young's modulus is dezelfde als de dimensie van druk (Pascal).
Elastische limiet
Volgens de definitie geeft de elasticiteitsmodulus aan hoeveel spanning op een vaste stof moet worden uitgeoefend om 100% te vervormen. Alle vaste stoffen hebben echter een elastische limiet gelijk aan 1% rek. Dit betekent dat als een geschikte kracht wordt uitgeoefend en het lichaam wordt vervormd met een hoeveelheid van minder dan 1%, het lichaam na beëindiging van deze kracht precies zijn oorspronkelijke vorm en afmetingen herstelt. Als er te veel kracht wordt uitgeoefend, waarbij de vervormingswaarde groter is dan 1%, zal het lichaam na beëindiging van de externe kracht niet meer zijn oorspronkelijke afmetingen herstellen. In het laatste geval spreekt men van het bestaan van een restvervorming, namelijk:bewijs dat de elastische limiet van het materiaal is overschreden.
Young's modulus in actie
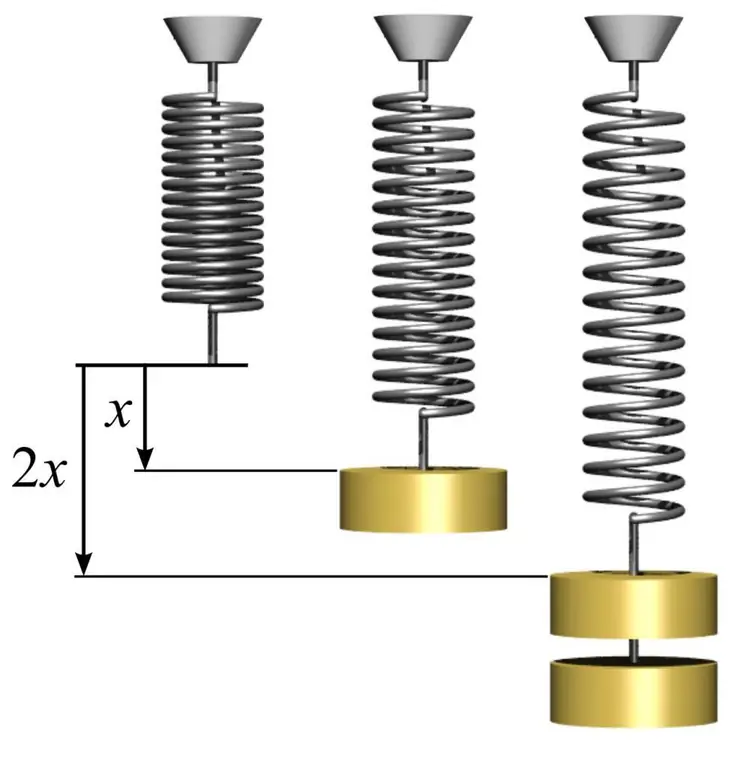
Om de elasticiteitsmodulus te bepalen en om te begrijpen hoe u deze moet gebruiken, kunt u een eenvoudig voorbeeld geven met een veer. Om dit te doen, moet u een metalen veer nemen en het gebied meten van de cirkel die de spoelen vormen. Dit wordt gedaan met behulp van de eenvoudige formule S=πr², waarbij n pi gelijk is aan 3,14 en r de straal van de spoel van de veer is.
Meet vervolgens de lengte van de veer l0 zonder belasting. Als je een lading met massa m1 aan een veer hangt, dan zal deze in lengte toenemen tot een bepaalde waarde l1. De elasticiteitsmodulus E kan worden berekend op basis van kennis van de wet van Hooke met de formule: E=m1gl0/(S(l 1-l0)), waarbij g de vrije valversnelling is. In dit geval merken we op dat de mate van vervorming van de veer in het elastische gebied ruim 1% kan overschrijden.
Als je de modulus van Young kent, kun je de hoeveelheid vervorming voorspellen onder invloed van een bepaalde spanning. In dit geval, als we een andere massa m2 aan de veer hangen, krijgen we de volgende waarde van relatieve vervorming: d=m2g/ (SE), waarbij d - relatieve vervorming in het elastische gebied.
Isotropie en anisotropie
Elasticiteitsmodulus is een kenmerk van een materiaal dat de sterkte van de binding tussen zijn atomen en moleculen beschrijft, maar een bepaald materiaal kan verschillende Young's moduli hebben.
Het feit is dat de eigenschappen van elke vaste stof afhangen van zijn interne structuur. Als de eigenschappen in alle ruimtelijke richtingen hetzelfde zijn, dan hebben we het over een isotroop materiaal. Dergelijke stoffen hebben een homogene structuur, dus de inwerking van een externe kracht in verschillende richtingen op hen veroorzaakt dezelfde reactie van het materiaal. Alle amorfe materialen zijn isotroop, zoals rubber of glas.
Anisotropie is een fenomeen dat wordt gekenmerkt door de afhankelijkheid van de fysische eigenschappen van een vaste stof of vloeistof van richting. Alle metalen en legeringen die daarop zijn gebaseerd, hebben een of ander kristalrooster, dat wil zeggen een geordende, in plaats van een chaotische opstelling van ionische kernen. Voor dergelijke materialen varieert de elasticiteitsmodulus afhankelijk van de werkingsas van de externe spanning. Metalen met kubische symmetrie, zoals aluminium, koper, zilver, vuurvaste metalen en andere, hebben bijvoorbeeld drie verschillende Young's moduli.
Afschuifmodulus
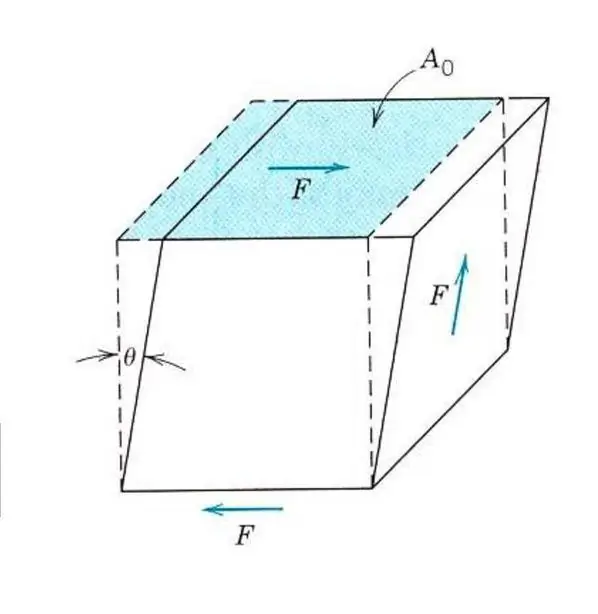
Beschrijving van de elastische eigenschappen van zelfs een isotroop materiaal vereist geen kennis van één Young's modulus. Want naast trek en druk kan het materiaal ook onderhevig zijn aan schuifspanningen of torsiespanningen. In dit geval zal het anders reageren op externe kracht. Om elastische afschuifvervorming te beschrijven, wordt een analoog van Young's modulus, afschuifmodulus of elasticiteitsmodulus van de tweede soort geïntroduceerd.
Alle materialen zijn minder bestand tegen schuifspanningen dan trek of druk, dus de waarde van de afschuifmodulus is 2-3 keer lager dan de waarde van de Young's modulus. Dus voor titanium, waarvan de Young's modulus gelijk is aan 107 GPa, is de afschuifmodulusslechts 40 GPa, voor staal zijn deze cijfers respectievelijk 210 GPa en 80 GPa.
Elasticiteitsmodulus van hout

Hout is een anisotroop materiaal omdat houtvezels in een specifieke richting zijn georiënteerd. Het is langs de vezels dat de elasticiteitsmodulus van hout wordt gemeten, aangezien deze over de vezels 1-2 orden van grootte kleiner is. Kennis van Young's modulus voor hout is belangrijk en er wordt rekening mee gehouden bij het ontwerpen van houten paneelconstructies.
De waarden van de elasticiteitsmodulus van hout voor sommige soorten bomen worden weergegeven in de onderstaande tabel.
| Boomaanzicht | Young's modulus in GPa |
| laurierboom | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Vuren | 11 |
| Dennen | 10 |
| Eiken | 12 |
Opgemerkt moet worden dat de gegeven waarden voor een bepaalde boom tot 1 GPa kunnen verschillen, aangezien de Young's modulus wordt beïnvloed door de dichtheid van het hout en de groeiomstandigheden.

Afschuifmoduli voor verschillende boomsoorten liggen in het bereik van 1-2 GPa, bijvoorbeeld voor dennen is het 1,21 GPa en voor eiken 1,38 GPa, dat wil zeggen dat hout praktisch geen weerstand biedt aan schuifspanningen. Met dit feit moet rekening worden gehouden bij de vervaardiging van houten dragende constructies, die zijn ontworpen om alleen onder spanning of druk te werken.
Elastische eigenschappen van metalen
In vergelijking met de Young's modulus van hout zijn de gemiddelde waarden van deze waarde voor metalen en legeringen een orde van grootte groter, zoals weergegeven in de volgende tabel.
| Metaal | Young's modulus in GPa |
| Brons | 120 |
| Koper | 110 |
| Staal | 210 |
| Titanium | 107 |
| Nikkel | 204 |
Elastische eigenschappen van metalen met een kubische syngonie worden beschreven door drie elastische constanten. Dergelijke metalen omvatten koper, nikkel, aluminium, ijzer. Als een metaal een hexagonale syngonie heeft, dan zijn er al zes constanten nodig om zijn elastische eigenschappen te beschrijven.
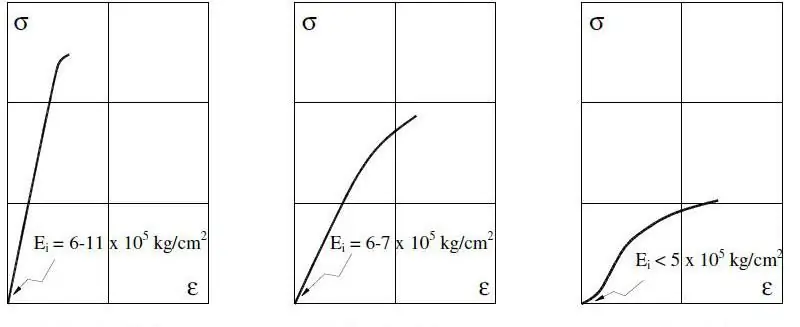
Voor metalen systemen wordt de Young's modulus gemeten binnen 0,2% rek, omdat er al grote waarden kunnen optreden in het inelastische gebied.






