Fouten zijn afwijkingen van meetresultaten van de werkelijke waarde van een grootheid. De werkelijke waarde kan alleen worden vastgesteld door talrijke metingen uit te voeren. In de praktijk is dit onmogelijk te implementeren.
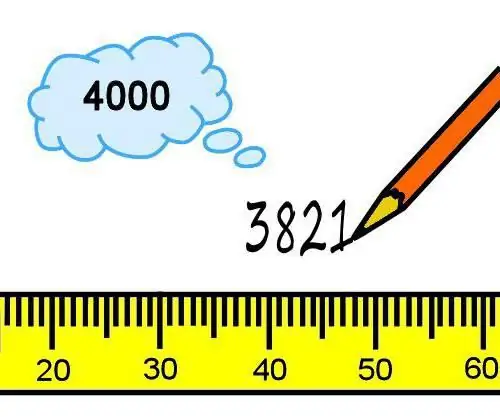
Voor de analyse van afwijkingen wordt de waarde die het dichtst bij de werkelijke waarde ligt, beschouwd als de werkelijke waarde van de gemeten waarde. Het wordt verkregen met behulp van zeer nauwkeurige meetinstrumenten en -methoden. Voor het gemak van metingen, om ervoor te zorgen dat afwijkingen kunnen worden geëlimineerd, worden verschillende classificaties van fouten gebruikt. Overweeg de hoofdgroepen.
Uitdrukkingsmethode
Als we de fouten van meetinstrumenten op deze basis classificeren, kunnen we het volgende onderscheiden:
- Absolute afwijkingen. Ze worden uitgedrukt in eenheden van de hoeveelheid die wordt gemeten.
- Relatieve afwijking. Het wordt uitgedrukt door de verhouding van de absolute fout en het meetresultaat of de werkelijke waarde van de gemeten hoeveelheid.
- Gereduceerde afwijking. Het is de relatieve fout uitgedruktde verhouding van de absolute afwijking van het meetinstrument en de waarde die als constante indicator wordt genomen over het gehele bereik van de overeenkomstige meting. Zijn keuze is gebaseerd op GOST 8.009-84.
Voor veel meetinstrumenten wordt een nauwkeurigheidsklasse vastgesteld. De gegeven fout wordt geïntroduceerd omdat de relatieve waarde de afwijking alleen op een specifiek punt op de schaal kenmerkt en afhangt van de parameter van de gemeten waarde.

Voorwaarden en bronnen
De belangrijkste en aanvullende afwijkingen worden onderscheiden in de classificatie van fouten volgens deze criteria.
De eerste zijn de fouten van meetinstrumenten onder normale gebruiksomstandigheden. De belangrijkste afwijkingen zijn te wijten aan de imperfectie van de conversiefunctie, de imperfectie van de eigenschappen van de apparaten. Ze weerspiegelen het verschil tussen de werkelijke conversiefunctie van het apparaat onder normale omstandigheden en de nominale (vastgesteld in regelgevende documenten (technische voorwaarden, normen, enz.)).
Extra fouten treden op wanneer een waarde afwijkt van de normwaarde of doordat deze de grenzen van het genormaliseerde gebied overschrijdt.
Normale omstandigheden
De volgende normale parameters zijn gedefinieerd in de normatieve documentatie:
- Luchttemperatuur 20±5 deg.
- Relatieve vochtigheid 65±15%.
- Netspanning 220±4, 4 V.
- Voedingsfrequentie 50±1Hz.
- Geen magnetische of elektrische velden.
- De horizontale positie van het apparaat met een afwijking van ±2 graden.
Nauwkeurigheidsklasse
Tolerantielimieten van afwijkingen kunnen worden uitgedrukt in relatieve, absolute of gereduceerde fouten. Om het meest geschikte meetinstrument te kunnen kiezen, wordt een vergelijking gemaakt op basis van hun algemene kenmerk - de nauwkeurigheidsklasse. In de regel is dit de grens van toelaatbare basis- en aanvullende afwijkingen.

Met de nauwkeurigheidsklasse kunt u de limieten van de fouten van hetzelfde type meetinstrumenten begrijpen. Het kan echter niet worden beschouwd als een directe indicator van de nauwkeurigheid van de metingen die door elk van deze instrumenten worden uitgevoerd. Feit is dat andere factoren (voorwaarden, methode, etc.) ook van invloed zijn op de classificatie van meetfouten. Met deze omstandigheid moet rekening worden gehouden bij het kiezen van een meetinstrument, afhankelijk van de nauwkeurigheid die voor het experiment is gespecificeerd.
De waarde van de nauwkeurigheidsklasse wordt weerspiegeld in de technische voorwaarden, normen of andere regelgevende documenten. De vereiste parameter wordt geselecteerd uit het standaardbereik. Voor elektromechanische apparaten worden bijvoorbeeld de volgende waarden als normatief beschouwd: 0, 05, 0, 1, 0, 2, enz.
Als u de waarde van de nauwkeurigheidsklasse van het meetgereedschap kent, kunt u de toegestane waarde van de absolute afwijking voor alle delen van het meetbereik vinden. De indicator wordt meestal rechtstreeks op de schaal van het apparaat aangebracht.
De aard van verandering
Deze functie wordt gebruikt bij de classificatie van systematische fouten. Deze afwijkingen blijvenconstant of veranderen volgens bepaalde patronen bij het uitvoeren van metingen. Wijs in deze classificatie en soorten fouten toe die een systematisch karakter hebben. Deze omvatten: instrumentele, subjectieve, methodologische en andere afwijkingen.
Als de systematische fout nul nadert, wordt deze situatie correctheid genoemd.
Bij de classificatie van meetfouten in de metrologie worden ook willekeurige afwijkingen onderscheiden. Hun optreden kan niet worden voorspeld. Willekeurige fouten zijn niet verantwoordelijk; ze kunnen niet worden uitgesloten van het meetproces. Toevallige fouten hebben een grote impact op onderzoeksresultaten. Afwijkingen kunnen worden verminderd door herhaalde metingen met daaropvolgende statistische verwerking van de resultaten. Met andere woorden, de gemiddelde waarde die wordt verkregen uit herhaalde manipulaties zal dichter bij de echte parameter liggen dan die verkregen uit een enkele meting. Wanneer de willekeurige afwijking bijna nul is, spreken ze van de convergentie van de indicatoren van het meetapparaat.
Nog een groep fouten in de classificatie - missers. Ze worden in de regel geassocieerd met fouten gemaakt door de operator, of niet verklaard door de invloed van externe factoren. Missers worden meestal uitgesloten van de meetresultaten, er wordt geen rekening mee gehouden bij het verwerken van de ontvangen gegevens.
Afhankelijkheid van magnitude
De afwijking is mogelijk niet afhankelijk van de gemeten parameter of is daarmee niet evenredig. Dienovereenkomstig, bij de classificatie van fouten in metrologie, additieve enmultiplicatieve afwijkingen.
Deze laatste worden ook wel gevoeligheidsfouten genoemd. Additieve afwijkingen treden meestal op als gevolg van pickups, trillingen in steunen, wrijving en geluid. De multiplicatieve fout hangt samen met de onvolkomenheid van de afstelling van afzonderlijke onderdelen van de meetinstrumenten. Het kan op zijn beurt worden veroorzaakt door verschillende redenen, waaronder fysieke en veroudering van apparatuur.

Normalisering van kenmerken
Het wordt uitgevoerd afhankelijk van welke afwijking significant is. Als de additieve fout significant is, wordt de limiet genormaliseerd in de vorm van een verminderde afwijking, als deze multiplicatief is, wordt de formule voor de relatieve grootte van de verandering gebruikt.
Dit is een normalisatiemethode waarbij beide indicatoren vergelijkbaar zijn, dat wil zeggen dat de grens van het toelaatbare hoofdverschil wordt uitgedrukt in een formule met twee termen. Daarom bestaat de nauwkeurigheidsklasse-indicator ook uit 2 cijfers c en d in procenten, gescheiden door een schuine streep. Bijvoorbeeld 0,2/0,01. Het eerste getal geeft de relatieve fout weer onder normale omstandigheden. De tweede indicator karakteriseert de toename ervan met een toename van de waarde van X, d.w.z. weerspiegelt de invloed van de additieve fout.
Dynamiek van veranderingen in de gemeten indicator
In de praktijk wordt de classificatie van fouten gebruikt, die de aard van veranderingen in de gemeten hoeveelheid weerspiegelt. Het gaat om de scheiding van afwijkingen:
- Naar statische. Dergelijke fouten ontstaan bij langzaam veranderende ofverandert helemaal niet.
- Dynamisch. Ze verschijnen bij het meten van fysieke grootheden die snel veranderen in de tijd.
Dynamische afwijking is te wijten aan de traagheid van het apparaat.
Kenmerken van het schatten van afwijkingen
Moderne benaderingen voor de analyse en classificatie van fouten zijn gebaseerd op principes die ervoor zorgen dat wordt voldaan aan de vereisten voor de uniformiteit van metingen.
Om de doelen van beoordeling en onderzoek te bereiken, wordt de afwijking beschreven met behulp van een model (willekeurig, instrumenteel, methodologisch, enz.). Het definieert de kenmerken die kunnen worden gebruikt om de eigenschappen van de fout te kwantificeren. In de loop van de informatieverwerking is het noodzakelijk om schattingen van dergelijke kenmerken te vinden.

Het model is gekozen rekening houdend met de gegevens over de bronnen, inclusief de gegevens die tijdens het experiment zijn verkregen. Modellen zijn onderverdeeld in niet-deterministisch (willekeurig) en deterministisch. Deze laatste zijn respectievelijk geschikt voor systematische afwijkingen.
Het algemene model voor de willekeurige fout is de waarde die de kansverdelingsfunctie implementeert. Afwijkingskenmerken zijn in dit geval onderverdeeld in interval en punt. Bij het beschrijven van de fout van meetresultaten worden meestal intervalparameters gebruikt. Dit betekent dat de grenzen waarbinnen de afwijking kan worden gelokaliseerd, zijn gedefinieerd als overeenkomend met een bepaalde waarschijnlijkheid. In een dergelijke situatie worden de grenzen vertrouwen genoemd, en de waarschijnlijkheid respectievelijk vertrouwen.
Puntkenmerken worden gebruikt in gevallen waar het niet nodig of mogelijk is om de betrouwbaarheidsgrenzen van de afwijking te schatten.
Evaluatieprincipes
Bij het kiezen van afwijkingsschattingen worden de volgende voorzieningen gebruikt:
- Individuele parameters en eigenschappen van het geselecteerde model worden gekarakteriseerd. Dit komt doordat de deviatiemodellen een complexe structuur hebben. Er worden veel parameters gebruikt om ze te beschrijven. Hun vastberadenheid is vaak erg moeilijk, en in sommige situaties zelfs onmogelijk. Bovendien bevat de volledige beschrijving van het model in veel gevallen overbodige informatie, terwijl de kennis van individuele kenmerken voldoende zal zijn om de taken uit te voeren en de doelen van het experiment te bereiken.
- Schattingen van afwijkingen worden bij benadering bepaald. De nauwkeurigheid van de kenmerken komt overeen met het doel van de metingen. Dit is te wijten aan het feit dat de fout alleen de zone van onzekerheid van het resultaat kenmerkt en dat de uiteindelijke nauwkeurigheid niet nodig is.
- Afwijking is beter te overdrijven dan te onderschatten. In het eerste geval zal de kwaliteit van de meting afnemen, in het tweede geval is de volledige waardevermindering van de verkregen resultaten waarschijnlijk.

Geschatte fouten voor of na de meting. In het eerste geval wordt het a priori genoemd, in het tweede - a posteriori.






