Het bestuderen van de processen die plaatsvinden in statistische systemen wordt bemoeilijkt door de minimale grootte van deeltjes en hun enorme aantal. Het is praktisch onmogelijk om elk deeltje afzonderlijk te beschouwen, daarom worden statistische grootheden geïntroduceerd: de gemiddelde snelheid van deeltjes, hun concentratie, deeltjesmassa. De formule die de toestand van het systeem kenmerkt, rekening houdend met microscopische parameters, wordt de basisvergelijking van de moleculair-kinetische gastheorie (MKT) genoemd.
Een klein beetje over de gemiddelde deeltjessnelheid
Het bepalen van de snelheid van deeltjes werd eerst experimenteel uitgevoerd. Een bekend experiment uit het schoolcurriculum, uitgevoerd door Otto Stern, maakte het mogelijk om een idee te krijgen van deeltjessnelheden. Tijdens het experiment werd de beweging van zilveratomen in roterende cilinders bestudeerd: eerst, in een stationaire toestand van de installatie, dan wanneer deze met een bepaalde hoeksnelheid roteerde.
Als resultaat werd gevonden dat de snelheid van zilvermoleculen groter is dan de snelheid van het geluid en 500 m/s is. Het feit is heel interessant, omdat het voor een persoon moeilijk is om dergelijke bewegingssnelheden van deeltjes in stoffen te voelen.
Ideaal gas
Doorgaan met onderzoekHet lijkt alleen mogelijk in een systeem waarvan de parameters kunnen worden bepaald door directe metingen met behulp van fysieke instrumenten. Snelheid wordt gemeten met een snelheidsmeter, maar het idee om een snelheidsmeter aan een enkel deeltje te bevestigen is absurd. Alleen een macroscopische parameter die verband houdt met deeltjesbeweging kan direct worden gemeten.
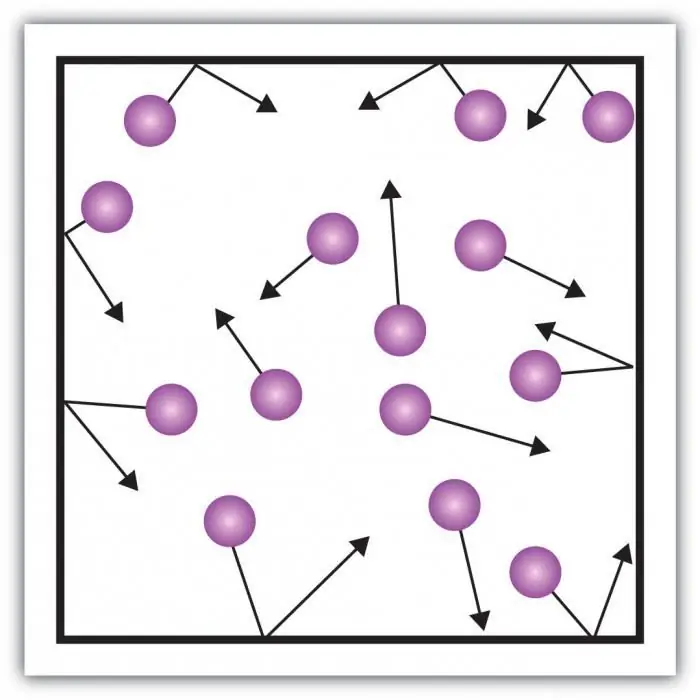
Houd rekening met gasdruk. De druk op de wanden van het vat wordt gecreëerd door de inslagen van de moleculen van het gas in het vat. De eigenaardigheid van de gasvormige toestand van materie is in voldoende grote afstanden tussen de deeltjes en hun kleine interactie met elkaar. Hierdoor kunt u direct de druk meten.
Elk systeem van op elkaar inwerkende lichamen wordt gekenmerkt door potentiële energie en kinetische bewegingsenergie. Echt gas is een complex systeem. De variabiliteit van potentiële energie leent zich niet voor systematisering. Het probleem kan worden opgelost door een model te introduceren dat de karakteristieke eigenschappen van het gas draagt en de complexiteit van de interactie opzij zet.
Ideaal gas is een toestand van materie waarin de interactie van deeltjes verwaarloosbaar is, de potentiële energie van interactie neigt naar nul. Alleen de bewegingsenergie, die afhangt van de snelheid van deeltjes, kan als significant worden beschouwd.
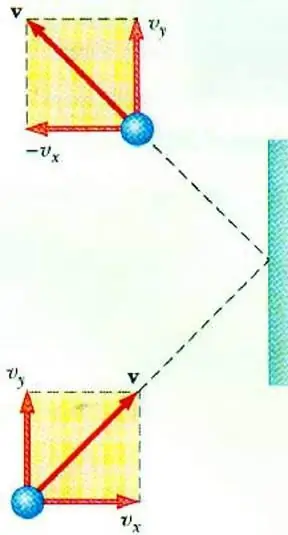
Ideale gasdruk
Om de relatie tussen gasdruk en de snelheid van zijn deeltjes te onthullen, is de basisvergelijking van de MKT van een ideaal gas mogelijk. Een deeltje dat in een vat beweegt, geeft bij botsing met de wand een impuls af, waarvan de waarde kan worden bepaald op basis van de tweede wetNewton:
F∆t=2m0vx
Verandering in het momentum van een deeltje tijdens elastische impact wordt geassocieerd met een verandering in de horizontale component van zijn snelheid. F is de kracht die korte tijd t vanaf de zijkant van het deeltje op de wand werkt; m0 - deeltjesmassa.
Alle gasdeeltjes botsen met het oppervlak van gebied S gedurende de tijd ∆t, bewegend in de richting van het oppervlak met snelheid vx en bevinden zich in een cilinder met volume Sυ x Δt. Bij deeltjesconcentratie n beweegt precies de helft van de moleculen naar de wand, de andere helft in de tegenovergestelde richting.
Na de botsing van alle deeltjes te hebben overwogen, kunnen we de wet van Newton schrijven voor de kracht die op het gebied werkt:
F∆t=nm0vx2S∆t
Aangezien gasdruk wordt gedefinieerd als de verhouding van de kracht die loodrecht op het oppervlak werkt tot het gebied van de laatste, kunnen we schrijven:
p=F: S=nm0vx2
De resulterende relatie als de basisvergelijking van de MKT kan niet het hele systeem beschrijven, omdat er maar één bewegingsrichting wordt beschouwd.
Maxwell-distributie
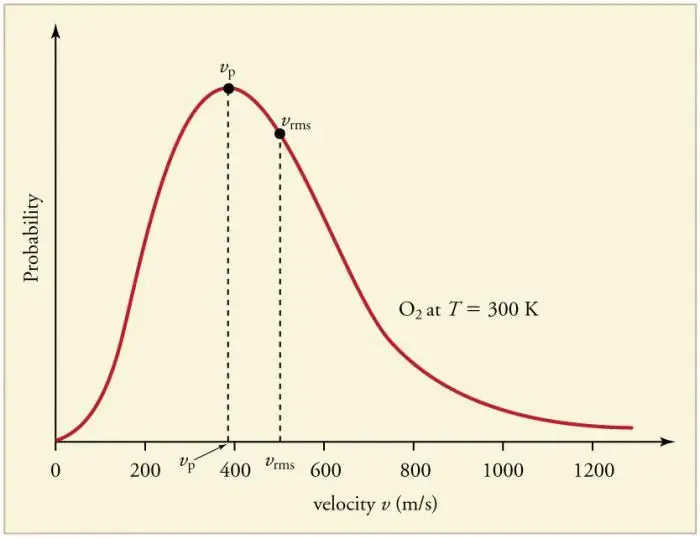
Continu frequente botsingen van gasdeeltjes met de wanden en met elkaar leiden tot de vaststelling van een bepaalde statistische verdeling van deeltjes in termen van snelheden (energieën). De richtingen van alle snelheidsvectoren blijken even waarschijnlijk te zijn. Deze verdeling wordt de Maxwell-verdeling genoemd. In 1860 was dit patroonafgeleid door J. Maxwell op basis van de MKT. De belangrijkste parameters van de distributiewet worden snelheden genoemd: waarschijnlijk, overeenkomend met de maximale waarde van de curve, en wortel-gemiddelde-kwadraat vkv=√‹v2 › - het gemiddelde kwadraat van de deeltjessnelheid.
Verhoging van de gastemperatuur komt overeen met een toename van de snelheid.
Gebaseerd op het feit dat alle snelheden gelijk zijn en hun modules dezelfde waarde hebben, kunnen we aannemen:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, van: ‹ vx2›=‹v2›: 3
De basisvergelijking van de MKT, rekening houdend met de gemiddelde waarde van de gasdruk, is:
p=nm0‹v2›: 3.
Deze relatie is uniek omdat het de relatie bepa alt tussen microscopische parameters: snelheid, deeltjesmassa, deeltjesconcentratie en gasdruk in het algemeen.
Door het concept van de kinetische energie van deeltjes te gebruiken, kan de basisvergelijking van de MKT anders worden herschreven:
p=2nm0‹v2›: 6=2n‹Ek›: 3
De druk van een gas is evenredig met de gemiddelde waarde van de kinetische energie van zijn deeltjes.
Temperatuur
Interessant is dat voor een constante hoeveelheid gas in een gesloten vat, men de gasdruk en de gemiddelde waarde van de deeltjesbewegingsenergie kan relateren. In dit geval kan de druk worden gemeten door de energie te metendeeltjes.
Wat te doen? Welke waarde kan worden vergeleken met kinetische energie? Temperatuur blijkt zo'n waarde te zijn.

Temperatuur is een maat voor de thermische toestand van stoffen. Om het te meten, wordt een thermometer gebruikt, waarvan de basis de thermische uitzetting van de werkvloeistof (alcohol, kwik) bij verhitting is. De thermometerschaal is experimenteel gemaakt. Gewoonlijk worden er markeringen op aangebracht die overeenkomen met de positie van de werkvloeistof tijdens een fysiek proces dat plaatsvindt in een constante thermische toestand (kokend water, smeltend ijs). Verschillende thermometers hebben verschillende schalen. Bijvoorbeeld Celsius, Fahrenheit.

Universele temperatuurschaal
Gasthermometers kunnen als interessanter worden beschouwd in termen van onafhankelijkheid van de eigenschappen van de werkvloeistof. Hun schaal is niet afhankelijk van het type gas dat wordt gebruikt. In een dergelijk apparaat kan men hypothetisch de temperatuur bepalen waarbij de gasdruk naar nul neigt. Uit berekeningen blijkt dat deze waarde overeenkomt met -273,15 oC. De temperatuurschaal (absolute temperatuurschaal of Kelvinschaal) werd in 1848 geïntroduceerd. De mogelijke temperatuur van nulgasdruk werd als het belangrijkste punt van deze schaal genomen. Een eenheidssegment van de schaal is gelijk aan een eenheidswaarde van de Celsius-schaal. Het lijkt handiger om de basis MKT-vergelijking op te schrijven met behulp van temperatuur bij het bestuderen van gasprocessen.
Relatie tussen druk en temperatuur
Empirisch kun je dat verifiërenevenredigheid van de gasdruk met zijn temperatuur. Tegelijkertijd werd gevonden dat de druk recht evenredig is met de concentratie van deeltjes:
P=nkT,
waar T de absolute temperatuur is, is k een constante gelijk aan 1,38•10-23J/K.
De fundamentele waarde, die een constante waarde heeft voor alle gassen, wordt de Boltzmann-constante genoemd.
Als we de afhankelijkheid van druk op temperatuur en de basisvergelijking van de MKT-gassen vergelijken, kunnen we schrijven:
‹Ek›=3kT: 2
De gemiddelde waarde van de kinetische energie van de beweging van gasmoleculen is evenredig met de temperatuur. Dat wil zeggen, temperatuur kan dienen als een maat voor de kinetische energie van deeltjesbeweging.

