Gewone breuken verkleinen wordt op school geleerd in wiskundelessen. Als je een student bent die dit onderwerp veilig heeft gemist of het niet heeft begrepen, of als je de ouder bent van zo'n student, dan is dit onderwerp iets voor jou. Hoe een breuk verkleinen? Makkelijk en eenvoudig als je de onderstaande methode volgt.
Wat is een gewone breuk
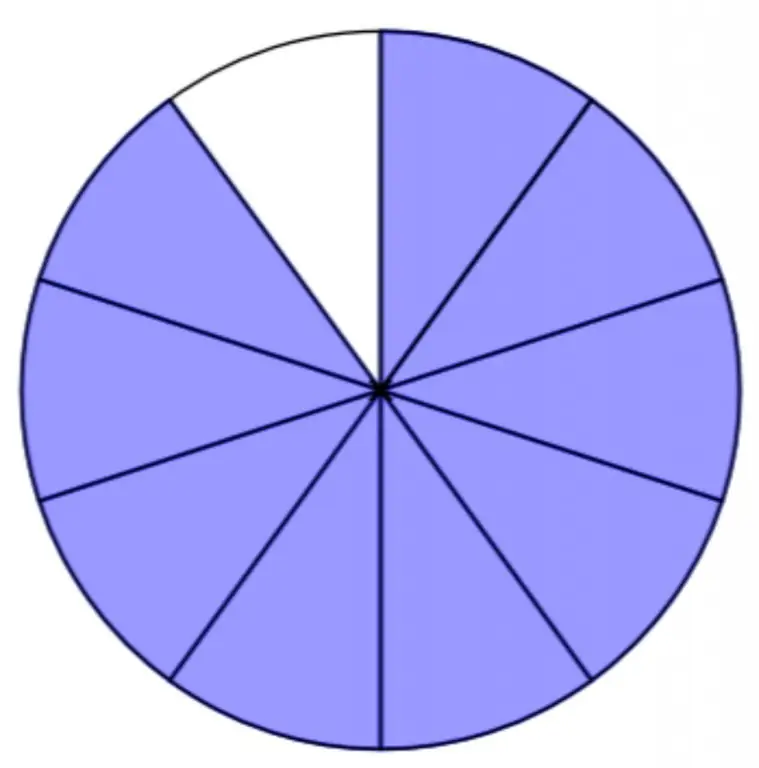
Herinner je de theorie. Gewone breuken verschijnen als gevolg van het verdelen van een object of meeteenheid in meerdere gelijke delen. Laten we taart als voorbeeld nemen. Als je het in tien delen snijdt en deze tien delen aan tien gasten geeft, dan ziet het er in een gewone fractie uit als 1/10 (een tiende). Maar op de brief wordt dit weerspiegeld in een invoer van twee verdiepingen, waarin een getal boven het streepje aangeeft hoeveel onderdelen er zijn genomen, en onder het streepje het totale aantal.
De breuk 2/5 betekent bijvoorbeeld dat een persoon slechts twee van de vijf delen van iets heeft genomen.
Laten we verder gaan met de hoofdvraag: hoe een breuk te verkleinen?
Wat betekent het
Een breuk verkleinen betekent de teller (het getal boven de lijn) en de noemer (het getal onder de lijn) door hetzelfde delenhetzelfde getal (het moet groter zijn dan één). Bovendien moet je delen totdat de teller en noemer een totaal aantal hebben waarmee ze kunnen worden gedeeld.
Verkleinde breuken zijn breuken die niet verder kunnen worden gereduceerd. Ze worden niet als verminderd beschouwd als de teller en noemer nog steeds een gemeenschappelijk getal hebben waardoor ze elk kunnen worden gedeeld.
Afkorting
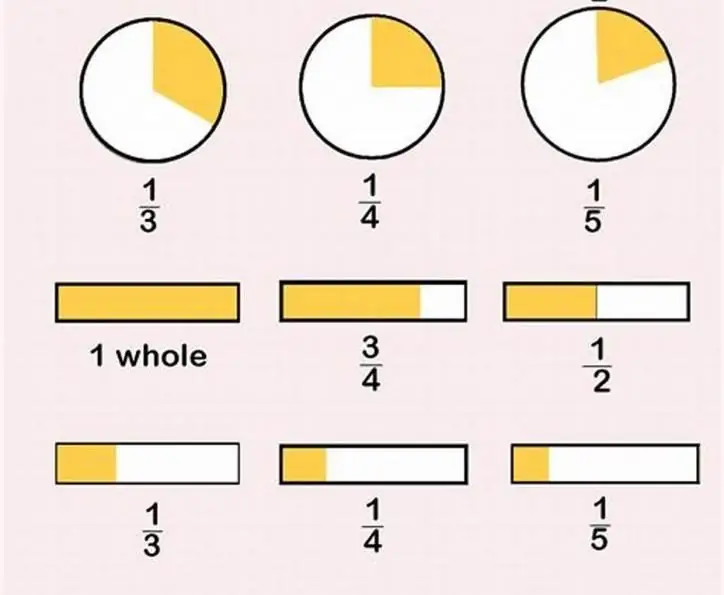
Dat is geregeld, laten we verder gaan met de volgende vraag. Laten we eens kijken naar voorbeelden van het verkleinen van een breuk.
Neem de breuk 25/5. Door welk getal delen we? Voor vijf. Laten we de teller en noemer ermee verkleinen. Het resultaat is het getal 1/5. Kun je verder knippen? Nee.
Of fractie 60/120. Door welk getal kunnen ze worden gedeeld? Voor dertig. We verkleinen en krijgen het getal 2/4. Kun je verder knippen? Ja, je kunt er nog twee snijden. Krijg 1/2.
Hoe verklein je de breuk "tot het winnende getal", dat wil zeggen, niet om het meerdere keren te delen? Probeer gewoon het grootste getal te vinden dat de teller en de noemer deelt. Toen we het tweede voorbeeld analyseerden, de breuk 60/120, kon deze worden gedeeld door zestig en onmiddellijk 1/2 krijgen.
Als het grootste getal niet meteen wordt gevonden, probeer dan eerst de breuk te delen door een willekeurig getal dat in je opkomt en probeer opnieuw met de nieuwe breuk te werken. Het belangrijkste is om de breuk correct en volledig te verminderen. Het maakt niet uit hoeveel stappen je neemt om er te komen, maar als je je tijd op prijs stelt, probeer het dan allemaal in één stap te doen.






