Ideaal gas, de ideale toestandsvergelijking voor gas, de temperatuur en druk, het volume… de lijst met parameters en definities die in het overeenkomstige deel van de natuurkunde worden gebruikt, kan nog heel lang worden voortgezet. Vandaag zullen we het alleen over dit onderwerp hebben.
Wat wordt beschouwd in de moleculaire fysica?

Het belangrijkste object dat in deze sectie wordt besproken, is een ideaal gas. De ideale toestandsvergelijking voor gas werd verkregen rekening houdend met normale omgevingsomstandigheden, en we zullen hier later over praten. Laten we dit "probleem" nu van een afstand benaderen.
Laten we zeggen dat we wat gas hebben. De toestand ervan kan worden bepaald met behulp van drie parameters van thermodynamische aard. Dit zijn natuurlijk druk, volume en temperatuur. De vergelijking van de toestand van het systeem is in dit geval de formule voor de relatie tussen de overeenkomstige parameters. Het ziet er als volgt uit: F (p, V, T)=0.
Hier, voor het eerst, naderen we langzaam de opkomst van zoiets als ideaalgas. Het wordt een gas genoemd waarin de interacties tussen moleculen verwaarloosbaar zijn. In de natuur komt dit over het algemeen niet voor. Elk zeer ijl gas is er echter dichtbij. Stikstof, zuurstof en lucht, die zich onder normale omstandigheden bevinden, verschillen weinig van het ideaal. Om de toestandsvergelijking voor een ideaal gas te schrijven, kunnen we de uniforme gaswet gebruiken. We krijgen: pV/T=const.
Gerelateerd concept 1: de wet van Avogadro
Hij kan ons vertellen dat als we hetzelfde aantal mol van absoluut willekeurig gas nemen en ze onder dezelfde omstandigheden plaatsen, inclusief temperatuur en druk, de gassen hetzelfde volume zullen innemen. In het bijzonder werd het experiment onder normale omstandigheden uitgevoerd. Dit betekent dat de temperatuur 273,15 Kelvin was, de druk was één atmosfeer (760 millimeter kwik of 101325 Pascal). Met deze parameters nam het gas een volume in dat gelijk was aan 22,4 liter. Daarom kunnen we zeggen dat voor één mol van elk gas de verhouding van numerieke parameters een constante waarde zal zijn. Daarom is er voor gekozen om dit getal de letter R te geven en het de universele gasconstante te noemen. Het is dus gelijk aan 8,31. De eenheid is J/molK.
Ideaal gas. De ideale toestandsvergelijking voor gas en de manipulatie ervan
Laten we proberen de formule te herschrijven. Om dit te doen, schrijven we het in deze vorm: pV=RT. Vervolgens voeren we een eenvoudige actie uit, vermenigvuldigen beide zijden van de vergelijking met een willekeurig aantal mol. We krijgen pVu=uRT. Laten we rekening houden met het feit dat het product van het molair volume ende hoeveelheid materie is gewoon het volume. Maar het aantal mol zal immers tegelijkertijd gelijk zijn aan het quotiënt van de massa en de molaire massa. Dit is precies hoe de Mendelejev-Clapeyron-vergelijking eruit ziet. Het geeft een duidelijk beeld van wat voor soort systeem een ideaal gas vormt. De toestandsvergelijking voor een ideaal gas zal de vorm aannemen: pV=mRT/M.
Leid de formule voor druk af
Laten we nog wat manipulaties doen met de verkregen uitdrukkingen. Om dit te doen, wordt de rechterkant van de Mendelejev-Clapeyron-vergelijking vermenigvuldigd en gedeeld door het Avogadro-getal. Nu kijken we zorgvuldig naar het product van de hoeveelheid stof door het Avogadro-getal. Dit is niets anders dan het totale aantal moleculen in het gas. Maar tegelijkertijd zal de verhouding van de universele gasconstante tot het Avogadro-getal gelijk zijn aan de Boltzmann-constante. Daarom kunnen formules voor druk als volgt worden geschreven: p=NkT/V of p=nkT. Hier is het symbool n de deeltjesconcentratie.
Ideale gasprocessen
In de moleculaire fysica bestaat er zoiets als isoprocessen. Dit zijn thermodynamische processen die plaatsvinden in het systeem bij een van de constante parameters. In dit geval moet ook de massa van de stof constant blijven. Laten we ze specifieker bekijken. Dus de wetten van een ideaal gas.
Druk blijft constant
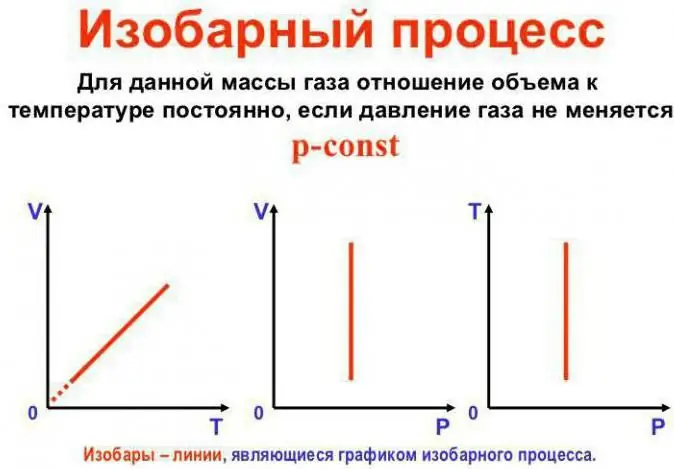
Dit is de wet van Gay-Lussac. Het ziet er als volgt uit: V/T=const. Het kan op een andere manier worden herschreven: V=Vo (1 + at). Hier is a gelijk aan 1/273,15 K^-1 en wordt de "volume-expansiecoëfficiënt" genoemd. We kunnen de temperatuur vervangen in zowel Celsius alsde Kelvin-schaal. In het laatste geval krijgen we de formule V=Voat.
Volume blijft constant

Dit is de tweede wet van Gay-Lussac, beter bekend als de wet van Charles. Het ziet er als volgt uit: p/T=const. Er is nog een andere formulering: p=po (1 + at). Transformaties kunnen worden uitgevoerd in overeenstemming met het vorige voorbeeld. Zoals je kunt zien, lijken de ideale gaswetten soms behoorlijk op elkaar.
Temperatuur blijft constant

Als de temperatuur van een ideaal gas constant blijft, kunnen we de wet van Boyle-Mariotte krijgen. Het kan als volgt worden geschreven: pV=const.
Gerelateerd concept 2: Gedeeltelijke druk
Laten we zeggen dat we een vat met gassen hebben. Het zal een mengsel zijn. Het systeem bevindt zich in een staat van thermisch evenwicht en de gassen zelf reageren niet met elkaar. Hierin staat N voor het totale aantal moleculen. N1, N2 enzovoort, respectievelijk het aantal moleculen in elk van de componenten van het mengsel. Laten we de drukformule p=nkT=NkT/V nemen. Het kan worden geopend voor een specifiek geval. Voor een tweecomponentenmengsel zal de formule de vorm aannemen: p=(N1 + N2) kT/V. Maar dan blijkt dat de totale druk wordt opgeteld bij de partiële drukken van elk mengsel. Het ziet er dus uit als p1 + p2 enzovoort. Dit zijn de partiële drukken.
Waar is het voor?
De formule die we hebben verkregen geeft aan dat de druk in het systeem afkomstig is van elke groep moleculen. Het is overigens niet afhankelijk vananderen. D alton profiteerde hiervan bij het formuleren van de later naar hem genoemde wet: in een mengsel waar gassen niet chemisch met elkaar reageren, zal de totale druk gelijk zijn aan de som van de partiële drukken.






