De natuurlijke fenomenen en processen om ons heen zijn behoorlijk complex. Voor hun exacte fysieke beschrijving moet een omslachtig wiskundig apparaat worden gebruikt en moet rekening worden gehouden met een groot aantal significante factoren. Om dit probleem te voorkomen, worden in de natuurkunde enkele vereenvoudigde modellen gebruikt, die de wiskundige analyse van het proces aanzienlijk vergemakkelijken, maar praktisch geen invloed hebben op de nauwkeurigheid van de beschrijving ervan. Een daarvan is het ideale gasmodel. Laten we het in meer detail bekijken in het artikel.
Het concept van een ideaal gas
Een ideaal gas is een aggregatietoestand van een stof, die bestaat uit materiële punten die geen interactie met elkaar hebben. Laten we deze definitie in meer detail uitleggen.
Ten eerste hebben we het over materiële punten als objecten waaruit een ideaal gas bestaat. Dit betekent dat zijn moleculen en atomen geen grootte hebben, maar een bepaalde massa. Het is veter kan een benadering worden gemaakt rekening houdend met het feit dat in alle reële gassen bij lage drukken en hoge temperaturen de afstand tussen moleculen veel groter is dan hun lineaire afmetingen.
Ten tweede mogen de moleculen in een ideaal gas geen interactie met elkaar aangaan. In werkelijkheid bestaan dergelijke interacties altijd. Dus zelfs atomen van edelgassen ervaren dipool-dipool aantrekking. Met andere woorden, er zijn van der Waals interacties aanwezig. Vergeleken met de kinetische energie van rotatie en translatiebeweging van moleculen, zijn deze interacties echter zo klein dat ze de eigenschappen van gassen niet beïnvloeden. Daarom kunnen ze niet worden overwogen bij het oplossen van praktische problemen.
Het is belangrijk op te merken dat niet alle gassen met een lage dichtheid en een hoge temperatuur als ideaal kunnen worden beschouwd. Naast van der Waals-interacties zijn er andere, sterkere soorten bindingen, bijvoorbeeld waterstofbruggen tussen H2O-moleculen, die leiden tot een grove schending van de ideale gasvoorwaarden. Om deze reden is waterdamp geen ideaal gas, maar lucht wel.
Fysiek model van een ideaal gas
Dit model kan als volgt worden weergegeven: stel dat het gassysteem N-deeltjes bevat. Dit kunnen atomen en moleculen zijn van verschillende chemicaliën en elementen. Het aantal N-deeltjes is groot, dus de eenheid "mol" wordt meestal gebruikt om het te beschrijven (1 mol komt overeen met het getal van Avogadro). Ze bewegen allemaal in een bepaald volume V. Deeltjesbewegingenzijn chaotisch en onafhankelijk van elkaar. Elk van hen heeft een bepaalde snelheid v en beweegt langs een recht pad.
Theoretisch is de kans op botsingen tussen deeltjes bijna nul, omdat hun grootte klein is in vergelijking met de afstanden tussen de deeltjes. Als een dergelijke botsing echter optreedt, is deze absoluut elastisch. In het laatste geval blijft het totale momentum van de deeltjes en hun kinetische energie behouden.
Het weloverwogen model van ideale gassen is een klassiek systeem met een enorm aantal elementen. Daarom gehoorzamen de snelheid en energie van deeltjes daarin aan de statistische verdeling van Maxwell-Boltzmann. Sommige deeltjes hebben lage snelheden, terwijl andere hoge snelheden hebben. In dit geval is er een bepaalde smalle snelheidslimiet, waarin de meest waarschijnlijke waarden van deze hoeveelheid liggen. De snelheidsverdeling van stikstofmoleculen is hieronder schematisch weergegeven.
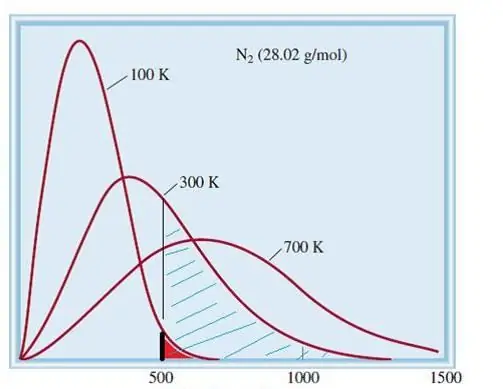
Kinetische theorie van gassen
Het hierboven beschreven model van ideale gassen bepa alt op unieke wijze de eigenschappen van gassen. Dit model werd voor het eerst voorgesteld door Daniel Bernoulli in 1738.

Vervolgens werd het ontwikkeld tot zijn huidige staat door August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski en andere wetenschappers.
De kinetische theorie van vloeibare stoffen, op basis waarvan het ideale gasmodel is gebouwd, verklaart twee belangrijke macroscopische eigenschappen van het systeem op basis van zijn microscopisch gedrag:
- De druk in gassen is het resultaat van de botsing van deeltjes met de wanden van het vat.
- De temperatuur in het systeem is het resultaat van de manifestatie van de constante beweging van moleculen en atomen.
Laten we beide conclusies van de kinetische theorie uitbreiden.
Gasdruk
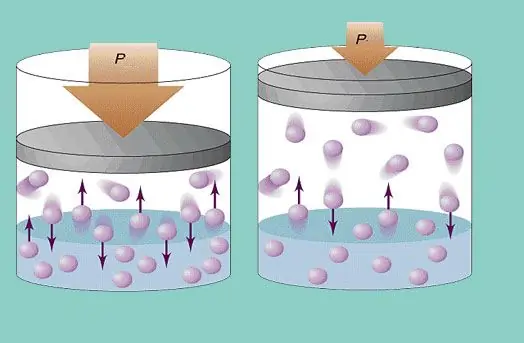
Het ideale gasmodel gaat uit van een constante chaotische beweging van deeltjes in het systeem en hun constante botsing met de wanden van het vat. Elke dergelijke botsing wordt als absoluut elastisch beschouwd. De deeltjesmassa is klein (≈10-27-10-25 kg). Daarom kan het bij een botsing niet veel druk uitoefenen. Niettemin is het aantal deeltjes, en dus het aantal botsingen, enorm (≈1023). Bovendien is de gemiddelde kwadratische snelheid van de elementen enkele honderden meters per seconde bij kamertemperatuur. Dit alles leidt tot het ontstaan van een merkbare druk op de wanden van het vat. Het kan worden berekend met behulp van de volgende formule:
P=Nmvcp2 / (3V), waar vcp de wortelgemiddelde kwadratische snelheid is, is m de deeltjesmassa.
Absolute temperatuur
Volgens het ideale gasmodel wordt de temperatuur op unieke wijze bepaald door de gemiddelde kinetische energie van een molecuul of atoom in het bestudeerde systeem. Je kunt de volgende uitdrukking schrijven die kinetische energie en absolute temperatuur voor een ideaal gas met elkaar in verband brengt:
mvcp2 / 2=3 / 2kB T.
Hier is kB de Boltzmann-constante. Uit deze gelijkheid krijgen we:
T=m vcp2 / (3kB).
Universele toestandsvergelijking
Als we de bovenstaande uitdrukkingen voor absolute druk P en absolute temperatuur T combineren, kunnen we de volgende gelijkheid schrijven:
PV=nRT.
Hier is n de hoeveelheid stof in mol, R is de gasconstante geïntroduceerd door D. I. Mendelejev. Deze uitdrukking is de belangrijkste vergelijking in de theorie van ideale gassen, omdat ze drie thermodynamische parameters (V, P, T) combineert en niet afhankelijk is van de chemische eigenschappen van het gassysteem.

De universele vergelijking werd voor het eerst experimenteel afgeleid door de Franse natuurkundige Emile Clapeyron in de 19e eeuw en vervolgens in zijn moderne vorm gebracht door de Russische chemicus Mendelejev, en daarom draagt het momenteel de namen van deze wetenschappers.






