De Titius-Bode-regel (soms eenvoudig de wet van Bode genoemd) is de hypothese dat lichamen in sommige orbitale systemen, waaronder de zon, langs halve assen roteren, afhankelijk van de planetaire volgorde. De formule suggereert dat elke planeet, zich naar buiten uitstrekkend, ongeveer twee keer zo ver van de zon zal zijn als de vorige.
De hypothese voorspelde correct de banen van Ceres (in de asteroïdengordel) en Uranus, maar kon de baan van Neptunus niet bepalen en werd uiteindelijk vervangen door de theorie van de vorming van het zonnestelsel. Het is vernoemd naar Johann Daniel Titius en Johann Elert Bode.

Oorsprong
De eerste vermelding van een serie die de wet van Bode benadert, is te vinden in Elements of Astronomy van David Gregory, gepubliceerd in 1715. Daarin zegt hij: "… aannemende dat de afstand van de zon tot de aarde is verdeeld in tien gelijke delen, waarvan de afstand van Mercurius ongeveer vier zal zijn, van Venus zeven, van Mars vijftien, van Jupiter tweeënvijftig, en van Saturnus vijfennegentig". Een soortgelijke suggestie, waarschijnlijk geïnspireerd door Gregory, verschijnt in een werk gepubliceerd door Christian Wolff in 1724.
In 1764 zei Charles Bonnet in zijn boek Contemplation of Nature: "We kennen de zeventien planeten waaruit ons zonnestelsel bestaat [dat wil zeggen, de belangrijkste planeten en hun satellieten], maar we weten niet zeker of ze zijn er niet meer." Hieraan voegde Johann Daniel Titius in zijn vertaling van Bonnets werk uit 1766 twee eigen paragrafen toe onderaan pagina 7 en bovenaan pagina 8. De nieuwe geïnterpoleerde paragraaf wordt niet gevonden in de originele tekst van Bonnet: noch in de Italiaanse noch Engelse vertalingen van het werk.
Ontdekking van Titius
Er zijn twee delen in de geïntercaleerde tekst van Titius. De eerste verklaart de opeenvolging van planetaire afstanden tot de zon. Het bevat ook een paar woorden over de afstand van de zon tot Jupiter. Maar dit is niet het einde van de tekst.
Het is de moeite waard om een paar woorden te zeggen over de formule van de Titius-Bode-regel. Let op de afstanden tussen de planeten en ontdek dat ze bijna allemaal van elkaar zijn gescheiden in een verhouding die overeenkomt met hun lichaamsgrootte. Deel de afstand van de zon tot Saturnus door 100 delen; dan is Mercurius door vier van dergelijke delen gescheiden van de zon; Venus - in 4 + 3=7 van dergelijke delen; Aarde - met 4+6=10; Mars - met 4+12=16.
Maar merk op dat er van Mars naar Jupiter een afwijking is van deze zo nauwkeurige voortgang. Vanaf Mars volgt een ruimte van 4+24=28 van zulke delen, maar daar is tot nu toe nog geen enkele planeet ontdekt. Maar moet de Lord Architect deze plek leeg laten? Nooit. Duslaten we aannemen dat deze ruimte zonder twijfel tot de nog onontdekte manen van Mars behoort, en eraan toevoegen dat Jupiter misschien nog een paar kleinere manen om zich heen heeft die nog niet door een telescoop zijn gezien.

Rise of the Bode
In 1772 voltooide Johann Elert Bode, op vijfentwintigjarige leeftijd, de tweede editie van zijn astronomische compendium Anleitung zur Kenntniss des gestirnten Himmels ("Gids voor de kennis van de sterrenhemel"), waaraan hij de volgende voetnoot toegevoegd, oorspronkelijk zonder bronnen, maar vermeld in latere versies. In Bode's memoires kan men een verwijzing naar Titius vinden met een duidelijke erkenning van zijn gezag.

Opinion Bode
Zo klinkt de Titius-Bode-regel in de presentatie van de laatste: als de afstand van de zon tot Saturnus gelijk is aan 100, dan is Mercurius door vier van dergelijke delen van de zon gescheiden. Venus - 4+3=7. Aarde - 4+6=10. Mars - 4+12=16.
Nu is er een gat in deze geordende progressie. Na Mars volgt een ruimte met een berekening van 4+24=28, waarin nog geen enkele planeet is gezien. Kunnen we geloven dat de grondlegger van het universum deze ruimte leeg heeft achtergelaten? Natuurlijk niet. Vanaf hier komen we tot de afstand van Jupiter in de vorm van berekening 4+48=52 en tenslotte tot de afstand van Saturnus - 4+96=100.

Deze twee uitspraken met betrekking tot alle specifieke typologie en orbitale stralen lijken uit de oudheid te komenastronomie. Veel van deze theorieën dateren van voor de zeventiende eeuw.
Invloed
Titius was een leerling van de Duitse filosoof Christian Freiherr von Wolff (1679-1754). Het tweede deel van de ingevoegde tekst in het werk van Bonnet is gebaseerd op het werk van Von Wolff uit 1723, Vernünftige Gedanken von den Wirkungen der Natur.
Twintigste-eeuwse literatuur wijst het auteurschap van de Titius-Bode-regel toe aan een Duitse filosoof. Zo ja, dan zou Titius van hem kunnen leren. Een andere oudere referentie is geschreven door James Gregory in 1702 in zijn Astronomiae Physicae et geometrieae Elementa, waar de reeks planetaire afstanden 4, 7, 10, 16, 52 en 100 een geometrische progressie werd van de verhouding 2.
Dit is de formule van Newton die het dichtst in de buurt komt en werd ook gevonden in de geschriften van Benjamin Martin en Thomas Ceard, jaren voordat Bonnets boek in Duitsland werd gepubliceerd.
Verdere werkzaamheden en praktische implicaties
Titius en Bode hoopten dat de wet zou leiden tot de ontdekking van nieuwe planeten, en inderdaad, de ontdekking van Uranus en Ceres, waarvan de afstand goed overeenkomt met de wet, droeg bij aan de acceptatie ervan door de wetenschappelijke wereld.
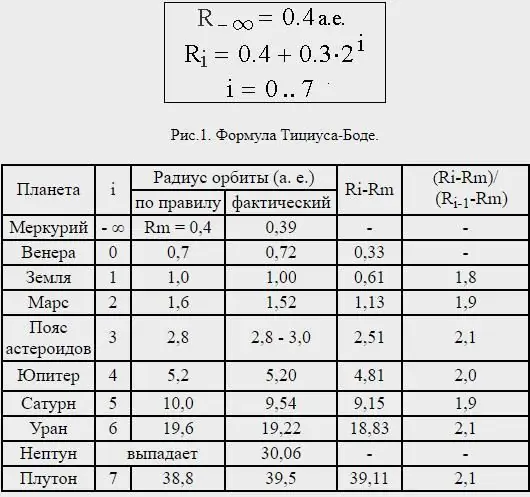
De afstand van Neptunus was echter erg inconsistent, en in feite bevindt Pluto - die nu niet als een planeet wordt beschouwd - zich op een gemiddelde afstand die ruwweg overeenkomt met de wet van Titius-Bode die voorspeld is voor de volgende planeet buiten Uranus.
Aan de oorspronkelijk gepubliceerde wet werd ongeveer voldaan door alle bekende planeten - Mercurius en Saturnus - met een opening tussenvierde en vijfde planeten. Dit werd tot de ontdekking van Uranus in 1781 als een interessant, maar niet van groot belang beschouwd, wat in de reeks past.
Op basis van deze ontdekking riep Bode op tot een zoektocht naar een vijfde planeet. Ceres, het grootste object in de asteroïdengordel, werd in 1801 gevonden op de voorspelde positie van Bode. De wet van Bode werd algemeen aanvaard totdat Neptunus in 1846 werd ontdekt en in strijd met de wet werd aangetoond.
Tegelijkertijd haalde een groot aantal asteroïden die in de gordel werden ontdekt Ceres uit de lijst met planeten. De wet van Bode werd in 1898 besproken door astronoom en logicus Charles Sanders Peirce als een voorbeeld van misleidend redeneren.

Ontwikkeling van het probleem
De ontdekking van Pluto in 1930 maakte het probleem nog ingewikkelder. Ook al kwam het niet overeen met de positie voorspeld door de wet van Bode, het ging over de positie die de wet voorspelde voor Neptunus. De daaropvolgende ontdekking van de Kuipergordel, en met name het object Eris, dat massiever is dan Pluto maar niet voldoet aan de wet van Bode, bracht de formule echter verder in diskrediet.
Serda's bijdrage
De jezuïet Thomas Cerda gaf de beroemde astronomiecursus in Barcelona in 1760 op de koninklijke leerstoel voor wiskunde aan het college van Sant Jaume de Cordelle (keizerlijk en koninklijk seminarie van de edelen van Cordell). In Cerdas' Tratado verschijnen planetaire afstanden, verkregen door de derde wet van Kepler toe te passen, met een nauwkeurigheid van 10-3.
Als we de afstand tot de aarde als 10 nemen ennaar boven afronden op geheel getal, geometrische progressie [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, van n=2 tot n=8, kan worden uitgedrukt. En met behulp van een cirkelvormige uniforme fictieve beweging naar de Kepler-anomalie, kunnen de Rn-waarden die overeenkomen met de verhoudingen van elke planeet worden verkregen als rn=(Rn - R1) / (Rn-1 - R1), wat resulteert in 1,82; 1, 84; 1, 86; 1,88 en 1,90, waarbij rn=2 - 0,02 (12 - n) een expliciete relatie is tussen de continuïteit van Kepler en de wet van Titius-Bode, die wordt beschouwd als een willekeurig numeriek toeval. Het resultaat van de berekening is bijna twee, maar de deuce kan heel goed worden beschouwd als een afronding van het getal 1, 82.

De gemiddelde snelheid van de planeet van n=1 tot n=8 verkleint de afstand tot de zon en verschilt van de uniforme afname bij n=2 om te herstellen van n=7 (orbitale resonantie). Dit heeft invloed op de afstand van de zon tot Jupiter. De afstand tussen alle andere objecten in het kader van de beruchte regel waaraan het artikel is gewijd, wordt echter ook bepaald door deze wiskundige dynamiek.
Theoretisch aspect
Er is geen solide theoretische verklaring die ten grondslag ligt aan de Titius-Bode-regel, maar het is mogelijk dat, gezien de combinatie van orbitale resonantie en gebrek aan vrijheidsgraden, elk stabiel planetair systeem een grote kans heeft om het model te herhalen dat wordt beschreven in deze theorie door de twee wetenschappers.
Omdat dit een wiskundig toeval kan zijn en geen "natuurwet", wordt het soms een regel genoemd in plaats van een "wet". Astrofysicus Alan Boss stelt echter dat dit eenvoudig is:toeval, en het planetaire wetenschappelijke tijdschrift Icarus accepteert niet langer artikelen die proberen verbeterde versies van de "wet" te bieden.
Orbitale resonantie
Orbitale resonantie van grote baanlichamen creëert gebieden rond de zon die geen stabiele banen op lange termijn hebben. De simulatieresultaten van planeetvorming ondersteunen het idee dat een willekeurig gekozen stabiel planetair systeem waarschijnlijk voldoet aan de Titius-Bode-regel.

Dubrulle en Graner
Dubrulle en Graner toonden aan dat afstandsregels op basis van machtswetten een gevolg kunnen zijn van modellen van instortende wolken van planetaire systemen die twee symmetrieën hebben: rotatie-invariantie (de wolk en zijn inhoud zijn assymmetrisch) en schaalinvariantie (de wolk en de inhoud ziet er op alle schalen hetzelfde uit).
Dit laatste is een kenmerk van veel verschijnselen waarvan men denkt dat ze een rol spelen bij de vorming van planeten, zoals turbulentie. De afstand van de zon tot de planeten van het zonnestelsel, voorgesteld door Titius en Bode, werd niet herzien in het kader van de studies van Dubrulle en Graner.






