In de wiskunde is sommatie (aangegeven door het grote Griekse sigma-symbool) een reeks optellingen van getallen. Wat is het bedrag? Dit is het resultaat van een dergelijke actie. Als de getallen achter elkaar van links naar rechts worden opgeteld, is het tussenresultaat een gedeeltelijke som.
Wat is het bedrag?
De op te tellen getallen kunnen geheel getal, rationaal, reëel of complex zijn. Naast deze kunnen andere soorten waarden worden toegevoegd: vectoren, matrices, polynomen en in het algemeen elementen van een additieve groep (of zelfs een monoïde).
Als het aantal elementen van de termen eindig is, geeft de sommatie altijd een goed gedefinieerde waarde. De optelling van een oneindige reeks waarden wordt een reeks genoemd. De waarde ervan kan vaak worden bepaald met behulp van een limiet (hoewel de waarde soms oneindig kan zijn).
Sequenties
De optelling van getallen [3, 7, 2, 1] kan worden gedefinieerd door een uitdrukking waarvan de waarde de som is van de cijfers die erin zijn opgenomen, bijvoorbeeld 3 + 7 + 2 + 1=13. Aangezien de toevoegingassociatief hangt de som niet af van hoe de termen zijn gegroepeerd, bijvoorbeeld (3 + 7) + (2 + 1) en 3 + ((7 + 2) + 1) zijn beide gelijk aan negen, dus haakjes worden meestal weggelaten. Optellen is ook commutatief, dus het herschikken van de termen verandert de waarde van de som niet. Merk op dat deze eigenschap mogelijk niet werkt voor oneindige sommatie.

Er is geen speciale notatie voor het optellen van dit soort reeksen. Er is slechts een kleine nuance als er minder dan twee elementen zijn. De sommatie van een reeks van één lid bevat geen plusteken (het is niet te onderscheiden van de vorm van het getal zelf), en als er helemaal geen elementen zijn, kan het niet eens worden geschreven (maar in plaats daarvan kan het worden aangeduid met de waarde "0"). Als de termen van de reeks echter worden gespecificeerd door een specifiek patroon, zoals een functie, dan kan de sommatie-operator nuttig of zelfs essentieel zijn.
Opnemen
Om te begrijpen wat een som is, is het ook nodig om het uiterlijk ervan te analyseren.
Om een reeks gehele getallen van 1 tot 100 op te tellen, wordt vaak een uitdrukking gebruikt die een weglatingsteken bevat om de ontbrekende leden aan te geven: 1 + 2 + 3 + 4 + … + 99 + 100. Het patroon is vrij gemakkelijk te zien in dit voorbeeld. Voor complexere opties is het echter noodzakelijk om precies de regel te specificeren die wordt gebruikt om de waarde van de elementen te vinden, wat kan worden bereikt met behulp van de sommatie-operator "Σ". Met dit symbool (sigma) kunt u de volgende notatie toepassen:
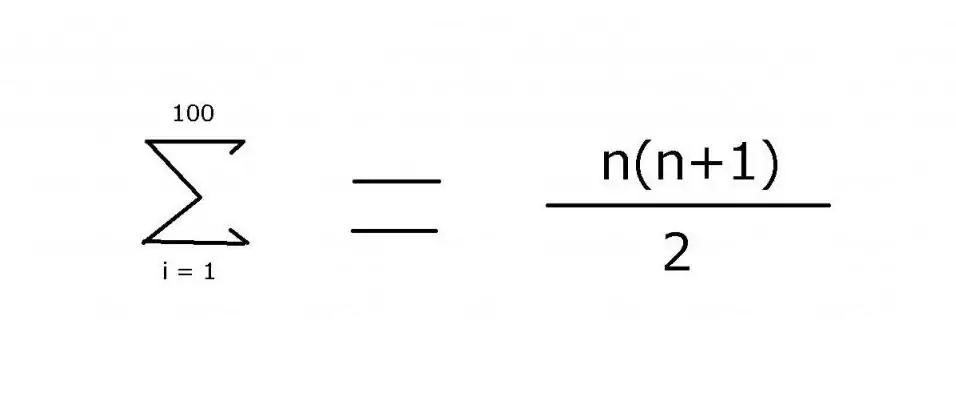
De waarde van deze uitdrukking is 5050. Het kan worden gevonden met behulp van wiskundige inductie, waar het tweede deel van de formule vandaan komt.
Voor verschillende reeksen zal de formule veranderen. Het opnameproces wordt gereduceerd tot het zoeken naar het voorbeeld van een oneindige reeks en deze vervolgens beschrijven met een formule. Als je dit hebt gedaan, is het niet moeilijk om te begrijpen wat het bedrag in een bepaald geval is.
Als het nodig is om te verduidelijken dat getallen samen met hun tekens (plus of min) worden opgeteld, wordt de term algebraïsche som gebruikt. In de theorie van elektrische circuits houden de circuitwetten van Kirchhoff bijvoorbeeld rekening met de algebraïsche som van stromen in een netwerk van geleiders die op een punt samenkomen, waardoor tegengestelde tekens worden gegeven aan stromen die in en uit een knooppunt stromen.






