Het onderwerp van ons artikel van vandaag is de kinematica van een materieel punt. Waar gaat het over? Welke concepten komen erin voor en welke definitie moet aan deze term worden gegeven? We zullen vandaag proberen deze en vele andere vragen te beantwoorden.
Definitie en concept
Kinematica van een materieel punt is niets meer dan een onderafdeling van de natuurkunde die 'mechanica' wordt genoemd. Zij bestudeert op haar beurt de bewegingspatronen van bepaalde lichamen. De kinematica van een materieel punt behandelt dit probleem ook, maar doet het niet op een algemene manier. In feite bestudeert deze subsectie methoden waarmee je de beweging van lichamen kunt beschrijven. In dit geval zijn alleen de zogenaamde geïdealiseerde lichamen geschikt voor onderzoek. Deze omvatten: een materieel punt, een absoluut stijf lichaam en een ideaal gas. Laten we de concepten in meer detail bekijken. We weten allemaal van de schoolbank dat het gebruikelijk is om een stoffelijk punt een lichaam te noemen, waarvan de afmetingen in een gegeven situatie kunnen worden verwaarloosd. Trouwens, de kinematica van de translatiebeweging van een materieel punt begint voor de eerste keerverschijnen in natuurkundeboeken van de zevende klas. Dit is de eenvoudigste tak, dus het is het handigst om met zijn hulp kennis te maken met de wetenschap. Een aparte vraag is wat de elementen zijn van de kinematica van een materieel punt. Er zijn er nogal wat, en voorwaardelijk kunnen ze worden onderverdeeld in verschillende niveaus met verschillende complexiteit om ze te begrijpen. Als we het bijvoorbeeld hebben over de straalvector, dan is er in principe niets onbetaalbaars in de definitie ervan. U zult het er echter mee eens zijn dat het voor een student veel gemakkelijker zal zijn om het te begrijpen dan voor een student van de middelbare of middelbare school. En om eerlijk te zijn, het is niet nodig om de kenmerken van deze term uit te leggen aan middelbare scholieren.
Een korte geschiedenis van het ontstaan van kinematica
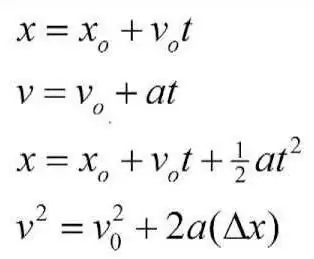
Vele, vele jaren geleden wijdde de grote wetenschapper Aristoteles het leeuwendeel van zijn vrije tijd aan de studie en beschrijving van natuurkunde als een afzonderlijke wetenschap. Hij werkte ook aan kinematica en probeerde de belangrijkste stellingen en concepten te presenteren, op de een of andere manier gebruikt bij pogingen om praktische en zelfs alledaagse problemen op te lossen. Aristoteles gaf de eerste ideeën over wat de elementen van de kinematica van een materieel punt zijn. Zijn werken en werken zijn zeer waardevol voor de hele mensheid. Niettemin maakte hij in zijn conclusies een aanzienlijk aantal fouten, en de reden hiervoor waren bepaalde misvattingen en misrekeningen. Op een gegeven moment raakte een andere wetenschapper, Galileo Galilei, geïnteresseerd in de werken van Aristoteles. Een van de fundamentele stellingen van Aristoteles was dat de beweging van een lichaamtreedt alleen op als er een kracht op inwerkt, bepaald door intensiteit en richting. Galileo bewees dat dit een vergissing was. De kracht heeft invloed op de parameter bewegingssnelheid, maar niet meer. De Italiaan toonde aan dat kracht de oorzaak is van versnelling, en dat het alleen onderling kan ontstaan. Galileo Galilei besteedde ook veel aandacht aan de studie van het proces van vrije val, waarbij de juiste patronen werden afgeleid. Waarschijnlijk herinnert iedereen zich zijn beroemde experimenten, die hij uitvoerde op de scheve toren van Pisa. De natuurkundige Ampère gebruikte ook de basis van kinematische oplossingen in zijn werken.
Initiële concepten
Zoals eerder vermeld, is kinematica de studie van manieren om de beweging van geïdealiseerde objecten te beschrijven. In dit geval kunnen de basisprincipes van wiskundige analyse, gewone algebra en geometrie in de praktijk worden toegepast. Maar welke concepten (precies concepten, en geen definities voor parametrische grootheden) liggen ten grondslag aan deze subsectie van de natuurkunde? Ten eerste moet iedereen duidelijk begrijpen dat de kinematica van de translatiebeweging van een materieel punt beweging beschouwt zonder rekening te houden met krachtindicatoren. Dat wil zeggen, om de overeenkomstige problemen op te lossen, hebben we geen formules nodig die verband houden met kracht. De kinematica houdt er geen rekening mee, hoeveel er ook zijn - één, twee, drie, minstens enkele honderdduizenden. Niettemin wordt nog steeds voorzien in het bestaan van versnelling. Bij een aantal problemen schrijft de kinematica van de beweging van een stoffelijk punt voor om de grootte van de versnelling te bepalen. De oorzaken van dit fenomeen (dat wil zeggen de krachten enhun aard) worden niet beschouwd, maar weggelaten.
Classificatie
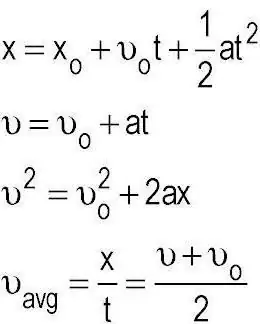
We ontdekten dat kinematica methoden onderzoekt en toepast om de beweging van lichamen te beschrijven zonder rekening te houden met de krachten die erop inwerken. Trouwens, een ander onderdeel van de mechanica, dat dynamiek wordt genoemd, behandelt zo'n taak. Daar worden al de wetten van Newton toegepast, waardoor in de praktijk heel wat parameters kunnen worden bepaald met een kleine hoeveelheid bekende initiële gegevens. De basisconcepten van de kinematica van een materieel punt zijn ruimte en tijd. En in verband met de ontwikkeling van de wetenschap, zowel in het algemeen als op dit gebied, rees de vraag over de geschiktheid van het gebruik van een dergelijke combinatie.
Vanaf het allereerste begin was er klassieke kinematica. We kunnen zeggen dat het niet alleen wordt gekenmerkt door de aanwezigheid van zowel tijdelijke als ruimtelijke hiaten, maar ook door hun onafhankelijkheid van de keuze van een of ander referentiekader. Trouwens, we zullen hier wat later over praten. Laten we nu even uitleggen waar we het over hebben. In dit geval wordt een segment als een ruimtelijk interval beschouwd en een tijdsinterval als een tijdsinterval. Alles lijkt duidelijk. Deze hiaten zullen in de klassieke kinematica dus worden beschouwd als absoluut, invariant, met andere woorden, onafhankelijk van de overgang van het ene referentiekader naar het andere. Of het nu gaat om bedrijfsrelativistische kinematica. Daarin kunnen de hiaten tijdens de overgang tussen referentiesystemen veranderen. Het zou zelfs juister zijn om te zeggen dat ze dat niet kunnen, maar ze moeten waarschijnlijk wel. Hierdoor is de gelijktijdigheid van de tweewillekeurige gebeurtenissen worden ook relatief en onderhevig aan speciale aandacht. Dat is de reden waarom in relativistische kinematica twee concepten - ruimte en tijd - worden gecombineerd tot één.
Kinematica van een materieel punt: snelheid, versnelling en andere grootheden
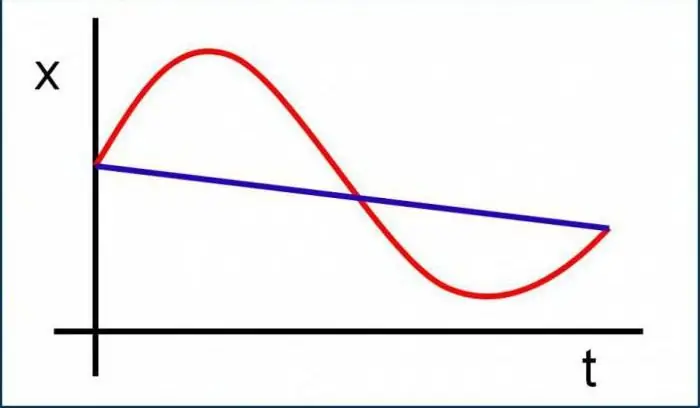
Om deze subsectie van de natuurkunde op zijn minst een beetje te begrijpen, moet je door de belangrijkste concepten navigeren, de definities kennen en je voorstellen wat deze of gene hoeveelheid in het algemeen is. Hier is niets moeilijks aan, sterker nog, alles is heel gemakkelijk en eenvoudig. Overweeg misschien om te beginnen de basisconcepten die worden gebruikt in kinematicaproblemen.
Beweging
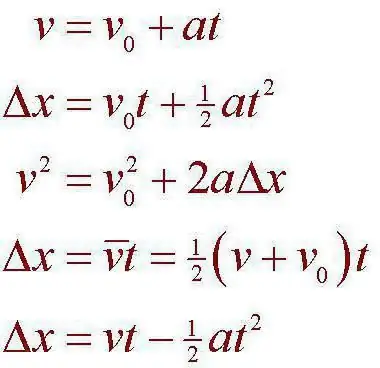
Mechanische beweging we zullen het proces beschouwen waarin een of ander geïdealiseerd object zijn positie in de ruimte verandert. In dit geval kunnen we zeggen dat de verandering optreedt ten opzichte van andere instanties. Het is ook noodzakelijk om rekening te houden met het feit dat het vaststellen van een bepaald tijdsinterval tussen twee gebeurtenissen tegelijkertijd plaatsvindt. Het zal bijvoorbeeld mogelijk zijn om een bepaald interval te isoleren dat is gevormd gedurende de tijd die verstrijkt tussen het aankomen van het lichaam van de ene positie naar de andere. We merken ook op dat de lichamen in dit geval met elkaar kunnen en zullen interageren, volgens de algemene wetten van de mechanica. Dit is precies waar de kinematica van een materieel punt meestal mee werkt. Het referentiesysteem is het volgende concept dat er onlosmakelijk mee verbonden is.
Coördinaten
Ze kunnen gewone gegevens worden genoemd waarmee u de positie van het lichaam op een of ander moment kunt bepalen. Coördinaten zijn onlosmakelijk verbonden met het concept van een referentiesysteem, evenals het coördinatenraster. Meestal zijn ze een combinatie van letters en cijfers.
Radius vector
Van de naam zou het al duidelijk moeten zijn wat het is. Laten we hier echter in meer detail over praten. Als een punt langs een bepaald traject beweegt, en we weten precies het begin van een bepaald referentiesysteem, dan kunnen we op elk moment een straalvector tekenen. Het verbindt de beginpositie van het punt met de momentane of eindpositie.
Traject
Het wordt een ononderbroken lijn genoemd, die wordt gelegd als gevolg van de beweging van een materieel punt in een bepaald referentiesysteem.
Snelheid (zowel lineair als hoekig)
Dit is een waarde die kan vertellen hoe snel het lichaam een bepaald afstandsinterval aflegt.
Versnelling (zowel hoekig als lineair)
Laat zien door welke wet en hoe intensief de snelheidsparameter van het lichaam verandert.
Misschien zijn ze hier - de belangrijkste elementen van de kinematica van een materieel punt. Opgemerkt moet worden dat zowel snelheid als versnelling vectorgrootheden zijn. En dat betekent dat ze niet alleen een indicatieve waarde hebben, maar ook een bepaalde richting. Trouwens, ze kunnen zowel in één richting als in tegengestelde richtingen worden gericht. In het eerste geval zal het lichaam versnellen, in het tweede geval zal het vertragen.
Eenvoudige taken
Kinematica van een materieel punt (snelheid, versnelling en afstand waarin praktisch fundamentele concepten zijn) omvat niet alleen een groot aantal taken, maar ook veel van hun verschillende categorieën. Laten we proberen een vrij eenvoudig probleem op te lossen door de door het lichaam afgelegde afstand te bepalen.
Stel dat de voorwaarden die we bij de hand hebben als volgt zijn. De auto van de bestuurder staat bij de startlijn. De telefoniste geeft het startsein met de vlag en de auto vertrekt abrupt. Bepaal of ze een nieuw record kan vestigen in de competitie van racers, als de volgende leider een afstand van honderd meter in 7,8 seconden aflegt. Neem de versnelling van de auto gelijk aan 3 meter gedeeld door een tweede kwadraat.
Dus, hoe dit probleem op te lossen? Het is best interessant, omdat we bepaalde parameters niet "droog" hoeven te bepalen. Het wordt opgefleurd met omzetten en een bepaalde situatie, wat het proces van oplossen en zoeken naar indicatoren diversifieert. Maar waar moeten we ons door laten leiden voordat we de taak benaderen?
1. De kinematica van een materieel punt voorziet in het gebruik van versnelling in dit geval.
2. De oplossing wordt aangenomen met behulp van de afstandsformule, aangezien de numerieke waarde ervan in de voorwaarden staat.
Het probleem is eigenlijk heel eenvoudig opgelost. Hiervoor nemen we de afstandsformule: S=VoT + (-) AT ^ 2/2. Wat is het nut? We moeten uitzoeken hoe lang de renner de aangegeven afstand zal afleggen, en dan het cijfer vergelijken met het record om erachter te komen of hij het verslaat of niet. Om dit te doen, tijd toewijzen, verkrijgen we de formulevoor hem: AT^2 + 2VoT - 2S. Dit is niets meer dan een kwadratische vergelijking. Maar de auto vertrekt, wat betekent dat de beginsnelheid 0 is. Bij het oplossen van de vergelijking is de discriminant gelijk aan 2400. Om de tijd te vinden, moet je de wortel nemen. Laten we het doen tot op de tweede decimaal: 48,98 Zoek de wortel van de vergelijking: 48,98/6=8,16 seconden. Het blijkt dat de coureur het bestaande record niet zal kunnen verbeteren.






