In de natuurkunde wordt het onderwerp parallelle en serieschakeling bestudeerd, en dit kunnen niet alleen geleiders zijn, maar ook condensatoren. Het is hier belangrijk om niet in de war te raken over hoe elk van hen eruitziet in het diagram. En pas dan specifieke formules toe. Trouwens, je moet ze uit je hoofd onthouden.
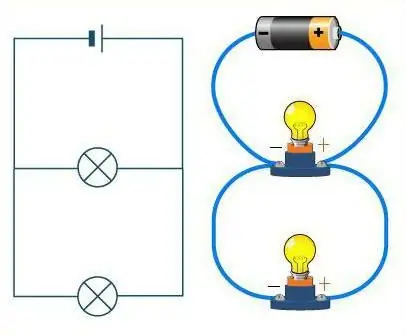
Hoe onderscheid te maken tussen deze twee verbindingen?
Bekijk het diagram goed. Als de draden worden weergegeven als een weg, zullen de auto's erop de rol van weerstanden spelen. Op een rechte weg zonder splitsingen rijden auto's de een na de ander in een ketting. Ook de serieschakeling van geleiders ziet er hetzelfde uit. De weg kan in dit geval een onbeperkt aantal bochten hebben, maar geen enkel kruispunt. Het maakt niet uit hoe de weg (draden) kwispelen, de machines (weerstanden) zullen altijd achter elkaar in één ketting worden geplaatst.
Het is een heel andere zaak als een parallelle verbinding wordt overwogen. Dan zijn de weerstanden te vergelijken met atleten aan de start. Zij zijnelk op zijn eigen baan, maar ze hebben dezelfde bewegingsrichting en de finishlijn ligt op dezelfde plaats. Evenzo weerstanden - elk van hen heeft zijn eigen draad, maar ze zijn allemaal op een bepaald punt verbonden.
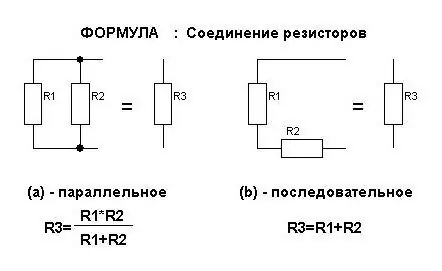
Formules voor huidige sterkte
Het wordt altijd besproken in het onderwerp "Elektriciteit". Parallelle en serieverbindingen beïnvloeden de hoeveelheid stroom in weerstanden op verschillende manieren. Voor hen worden formules afgeleid die onthouden kunnen worden. Maar het is voldoende om de betekenis te onthouden die erin is geïnvesteerd.
Dus de stroom in serieschakeling van geleiders is altijd hetzelfde. Dat wil zeggen, in elk van hen is de waarde van de huidige sterkte niet anders. Je kunt een analogie trekken als je een draad vergelijkt met een pijp. Daarin stroomt het water altijd op dezelfde manier. En alle obstakels op zijn pad zullen met dezelfde kracht worden weggevaagd. Zelfde met stroom. Daarom ziet de formule voor de totale stroom in een circuit met een serieschakeling van weerstanden er als volgt uit:
I gen=ik 1=ik 2
Hier geeft de letter I de kracht van de stroom aan. Dit is een veelgebruikte notatie, dus u moet deze onthouden.
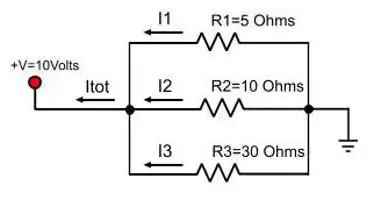
De stroom in parallelle verbinding zal niet langer een constante waarde zijn. Met dezelfde analogie met een pijp, blijkt dat het water in twee stromen wordt verdeeld als de hoofdpijp een aftakking heeft. Hetzelfde fenomeen wordt waargenomen met stroom wanneer een vertakking van draden op zijn pad verschijnt. De formule voor de totale stroomsterkte bij parallel geschakelde geleiders:
I gen=ik 1 + ik 2
Als de vertakking bestaat uit draden diemeer dan twee, dan zullen er in de bovenstaande formule meer termen met hetzelfde nummer zijn.
Formules voor stress
Wanneer een circuit wordt overwogen waarin de geleiders in serie zijn geschakeld, wordt de spanning in de hele sectie bepaald door de som van deze waarden op elke specifieke weerstand. Je kunt deze situatie vergelijken met platen. Het zal voor één persoon gemakkelijk zijn om een van hen vast te houden, hij zal ook in staat zijn om de tweede dichtbij te nemen, maar met moeite. Eén persoon zal niet langer drie borden naast elkaar kunnen houden, de hulp van een tweede zal nodig zijn. Enzovoort. De inspanningen van mensen tellen op.
De formule voor de totale spanning van een sectie van een circuit met een serieschakeling van geleiders ziet er als volgt uit:
U gen=U 1 + U 2, waarbij U de aangenomen aanduiding is voor elektrische spanning.
Een andere situatie doet zich voor als een parallelle aansluiting van weerstanden wordt overwogen. Wanneer borden op elkaar worden gestapeld, kunnen ze nog steeds door één persoon worden vastgehouden. U hoeft dus niets toe te voegen. Dezelfde analogie wordt waargenomen wanneer de geleiders parallel zijn geschakeld. De spanning op elk van hen is hetzelfde en gelijk aan die op allemaal tegelijk. De formule voor de totale spanning is:
U gen=U 1=U 2
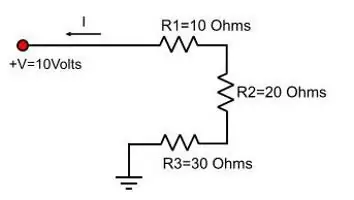
Formules voor elektrische weerstand
Je kunt ze niet meer onthouden, maar ken de formule van de wet van Ohm en leid er de gewenste uit af. Uit deze wet volgt dat:spanning is gelijk aan het product van stroom en weerstand. Dat wil zeggen, U=IR, waarbij R de weerstand is.
De formule waarmee u moet werken, hangt af van hoe de geleiders zijn aangesloten:
- in serie, dus je hebt gelijkheid nodig voor spanning - IgenRtotal=I1R1 + I2R2;
- parallel is het noodzakelijk om de formule voor de huidige sterkte te gebruiken - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Gevolgd door eenvoudige transformaties, die gebaseerd zijn op het feit dat in de eerste gelijkheid alle stromen dezelfde waarde hebben, en in de tweede - de spanningen gelijk zijn. Ze kunnen dus ingekort worden. Dat wil zeggen, de volgende uitdrukkingen worden verkregen:
- R gen=R 1 + R 2 (voor serieschakeling van geleiders)
- 1 / R gen=1 / R 1 + 1 / R 2(indien parallel aangesloten).
Als het aantal weerstanden dat op het netwerk is aangesloten toeneemt, verandert het aantal termen in deze uitdrukkingen.
Het is vermeldenswaard dat de parallelle en serieschakeling van geleiders een ander effect heeft op de totale weerstand. De eerste van hen vermindert de weerstand van het circuitgedeelte. Bovendien blijkt het minder te zijn dan de kleinste van de gebruikte weerstanden. Bij serieschakeling is alles logisch: de waarden tellen op, dus het totale aantal zal altijd het grootste zijn.
Werkstroom
De vorige drie grootheden vormen de wetten van parallelle verbinding en serieschakeling van geleiders in een circuit. Daarom is het noodzakelijk om ze te kennen. Over werk en macht, je hoeft alleen maar de basisformule te onthouden. Het is als volgt geschreven: A \u003d IUt, waarbij A het werk van de stroom is, t de tijd van zijn passage door de geleider.
Om het totale werk met een seriële verbinding te bepalen, moet u de spanning in de oorspronkelijke uitdrukking vervangen. Je krijgt de gelijkheid: A \u003d I(U 1 + U 2)t, door de haakjes te openen waarin blijkt dat de werk aan de hele sectie is gelijk aan het bedrag van elke specifieke huidige consument.
De redenering verloopt op dezelfde manier als een parallel verbindingsschema wordt overwogen. Alleen de huidige sterkte wordt verondersteld te worden vervangen. Maar het resultaat zal hetzelfde zijn: A=A 1 + A 2.
Huidige stroom
Bij het afleiden van een formule voor vermogen (notatie "P") van een circuitgedeelte, moet u opnieuw één formule gebruiken: P \u003d UI. Na zo'n redenering blijkt dat parallelle en serieverbindingen beschreven door een dergelijke formule voor macht: P \u003d P1 + P 2.
Dat wil zeggen, hoe de schema's ook worden opgesteld, het totale vermogen zal de som zijn van degenen die bij het werk betrokken zijn. Dit verklaart het feit dat het onmogelijk is om tegelijkertijd veel krachtige apparaten in het appartementsnetwerk op te nemen. Ze kan de lading gewoon niet aan.
Hoe beïnvloedt de aansluiting van geleiders de reparatie van de nieuwjaarsslinger?
Onmiddellijk nadat een van de lampen is doorgebrand, wordt duidelijk hoe ze waren aangesloten. Bijseriële verbinding, geen van hen zal oplichten. Dit komt doordat een onbruikbaar geworden lamp een breuk in het circuit veroorzaakt. Daarom moet je alles controleren om te bepalen welke is doorgebrand, deze vervangen - en de slinger zal beginnen te werken.
Als het een parallelle verbinding gebruikt, stopt het niet met werken als een van de lampen uitv alt. De ketting wordt immers niet helemaal gebroken, maar slechts één parallel deel. Om zo'n slinger te repareren, hoef je niet alle elementen van het circuit te controleren, maar alleen die elementen die niet gloeien.
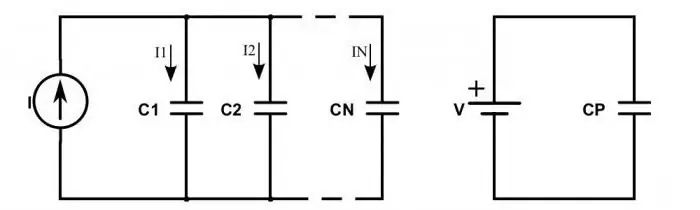
Wat gebeurt er met een circuit als er condensatoren worden gebruikt in plaats van weerstanden?
Wanneer ze in serie zijn geschakeld, wordt de volgende situatie waargenomen: ladingen van de plussen van de stroombron komen alleen naar de buitenste platen van de extreme condensatoren. Degenen daartussen geven die lading gewoon door aan de ketting. Dit verklaart het feit dat op alle platen dezelfde ladingen verschijnen, maar met verschillende tekens. Daarom kan de elektrische lading van elke in serie geschakelde condensator als volgt worden geschreven:
q gen =q 1=q 2.
Om de spanning op elke condensator te bepalen, moet je de formule kennen: U=q / C. Daarin is C de capaciteit van de condensator.
Totale spanning volgt dezelfde wet als weerstanden. Daarom, als we de spanning in de capaciteitsformule vervangen door de som, krijgen we dat de totale capaciteit van de apparaten moet worden berekend met behulp van de formule:
C=q / (U 1 + U2).
Je kunt deze formule vereenvoudigen door de breuken om te draaien en de verhouding tussen spanning en lading te vervangen door capaciteit. Het blijkt de volgende gelijkheid te zijn: 1 / С=1 / С 1 + 1 / С 2.
De situatie ziet er iets anders uit als de condensatoren parallel zijn geschakeld. Vervolgens wordt de totale lading bepaald door de som van alle ladingen die zich ophopen op de platen van alle apparaten. En de spanningswaarde wordt nog steeds bepaald volgens algemene wetten. Daarom is de formule voor de totale capaciteit van parallel geschakelde condensatoren:
С=(q 1 + q 2) / U.
Dat wil zeggen, deze waarde wordt beschouwd als de som van elk van de apparaten die in de verbinding worden gebruikt:
S=S 1 + S 2.
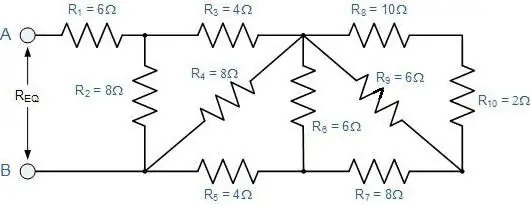
Hoe de totale weerstand van een willekeurige verbinding van geleiders bepalen?
Dat wil zeggen, een waarin opeenvolgende secties parallelle secties vervangen, en vice versa. Voor hen zijn alle beschreven wetten nog steeds geldig. U hoeft ze alleen in fasen toe te passen.
Ten eerste wordt verondersteld dat het het schema mentaal uitbreidt. Als het moeilijk voor te stellen is, moet je tekenen wat er gebeurt. De uitleg wordt duidelijker als we het bekijken met een specifiek voorbeeld (zie figuur).
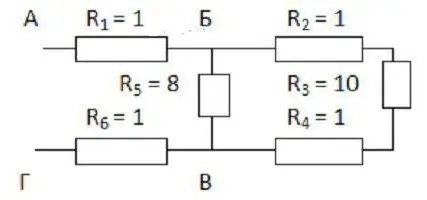
Het is handig om te beginnen met tekenen vanaf de punten B en C. Ze moeten op enige afstand van elkaar en van de randen van het vel worden geplaatst. Links nadert een draad punt B, en twee zijn al naar rechts gericht. Punt B daarentegen heeft twee vertakkingen aan de linkerkant en één draad erachter.
Nu moet je de ruimte tussen deze opvullenstippen. Drie weerstanden met coëfficiënten van 2, 3 en 4 moeten langs de bovenste draad worden geplaatst en die met een index van 5. De eerste drie zijn in serie verbonden. Met de vijfde weerstand staan ze parallel.
De resterende twee weerstanden (de eerste en zesde) zijn in serie verbonden met het beschouwde gedeelte van de BV. Daarom kan de tekening eenvoudig worden aangevuld met twee rechthoeken aan weerszijden van de geselecteerde punten. Het blijft om de formules toe te passen voor het berekenen van de weerstand:
- eerst degene die is opgegeven voor seriële verbinding;
- then voor parallel;
- en opnieuw voor opeenvolgende.
Op deze manier kunt u elk, zelfs zeer complex schema implementeren.
Het probleem van seriële aansluiting van geleiders
Conditie. Twee lampen en een weerstand zijn achter elkaar in een schakeling aangesloten. De totale spanning is 110 V en de stroom is 12 A. Wat is de waarde van de weerstand als elke lamp een vermogen van 40 V heeft?
Beslissing. Aangezien een serieschakeling wordt overwogen, zijn de formules voor de wetten bekend. Je hoeft ze alleen maar correct toe te passen. Begin met het vinden van de spanningswaarde over de weerstand. Om dit te doen, moet u twee keer de spanning van één lamp van het totaal aftrekken. Het blijkt 30 V te zijn.
Nu er twee grootheden bekend zijn, U en I (de tweede is gegeven in de voorwaarde, aangezien de totale stroom gelijk is aan de stroom in elke serieverbruiker), kunnen we de weerstand van de weerstand berekenen met De wet van Ohm. Het blijkt 2,5 ohm te zijn.
Antwoord. De weerstand van de weerstand is 2,5 ohm.
Taakvoor aansluiting van condensatoren, parallel en serie
Conditie. Er zijn drie condensatoren met capaciteiten van 20, 25 en 30 microfarad. Bepaal hun totale capaciteit wanneer ze in serie en parallel zijn aangesloten.
Beslissing. Het is gemakkelijker om te beginnen met een parallelle verbinding. In deze situatie hoeven alleen alle drie de waarden te worden toegevoegd. De totale capaciteit is dus 75uF.
De berekeningen zullen iets gecompliceerder zijn als deze condensatoren in serie zijn geschakeld. Je moet immers eerst de verhouding van eenheid tot elk van deze capaciteiten vinden en ze vervolgens bij elkaar optellen. Het blijkt dat de eenheid gedeeld door de totale capaciteit 37/300 is. Dan is de gewenste waarde ongeveer 8 microfarads.
Antwoord. De totale capaciteit in serieschakeling is 8 uF, parallel - 75 uF.






