Bij het bestuderen van de eigenschappen van een kwadratische vergelijking werd een beperking ingesteld - voor een discriminant kleiner dan nul is er geen oplossing. Er werd meteen bepaald dat we het hebben over een reeks reële getallen. De nieuwsgierige geest van een wiskundige zal geïnteresseerd zijn - wat is het geheim in de clausule over echte waarden?
Na verloop van tijd introduceerden wiskundigen het concept van complexe getallen, waarbij de voorwaardelijke waarde van de tweede wortel van min één als eenheid wordt genomen.
Historische achtergrond
Wiskundige theorie ontwikkelt zich sequentieel, van eenvoudig tot complex. Laten we eens kijken hoe het concept "complex getal" is ontstaan en waarom het nodig is.
Sinds onheuglijke tijden was de basis van de wiskunde het gebruikelijke verhaal. De onderzoekers kenden alleen de natuurlijke set van waarden. Optellen en aftrekken waren eenvoudig. Naarmate de economische verhoudingen complexer werden, begon men te vermenigvuldigen in plaats van dezelfde waarden toe te voegen. Er is een omgekeerde bewerking omvermenigvuldigen - delen.
Het concept van een natuurlijk getal beperkte het gebruik van rekenkundige bewerkingen. Het is onmogelijk om alle delingsproblemen op te lossen met de verzameling gehele getallen. Het werken met breuken leidde eerst tot het concept van rationele waarden en vervolgens tot irrationele waarden. Als het voor het rationele mogelijk is om de exacte locatie van het punt op de lijn aan te geven, dan is het voor het irrationele onmogelijk om zo'n punt aan te geven. U kunt het interval alleen benaderen. De vereniging van rationale en irrationele getallen vormde een reële verzameling, die kan worden weergegeven als een bepaalde lijn met een bepaalde schaal. Elke stap langs de lijn is een natuurlijk getal, en daartussen bevinden zich rationele en irrationele waarden.
Het tijdperk van de theoretische wiskunde is begonnen. De ontwikkeling van astronomie, mechanica en natuurkunde vereiste het oplossen van steeds complexere vergelijkingen. In het algemeen werden de wortels van de kwadratische vergelijking gevonden. Bij het oplossen van een complexere kubieke polynoom kwamen wetenschappers een tegenstrijdigheid tegen. Het concept van een derdemachtswortel van een negatief is logisch, maar voor een vierkantswortel wordt onzekerheid verkregen. Bovendien is de kwadratische vergelijking slechts een speciaal geval van de derdegraadsvergelijking.
In 1545 stelde de Italiaan J. Cardano voor om het concept van een denkbeeldig getal te introduceren.

Dit getal is de tweede wortel van min één. De term complex getal werd uiteindelijk pas driehonderd jaar later gevormd, in de werken van de beroemde wiskundige Gauss. Hij stelde voor om alle wetten van de algebra formeel uit te breiden tot het denkbeeldige getal. De echte lijn is verlengd totvliegtuigen. De wereld is groter.
Basisconcepten
Roep een aantal functies op die beperkingen hebben op de echte set:
- y=arcsin(x), gedefinieerd tussen negatief en positief 1.
- y=ln(x), decimale logaritme is logisch met positieve argumenten.
- vierkantswortel y=√x, alleen berekend voor x ≧ 0.
Aanduidend i=√(-1), introduceren we een concept als een denkbeeldig getal, dit verwijdert alle beperkingen uit het domein van de definitie van de bovenstaande functies. Uitdrukkingen zoals y=arcsin(2), y=ln(-4), y=√(-5) zijn logisch in een ruimte van complexe getallen.
De algebraïsche vorm kan worden geschreven als een uitdrukking z=x + i×y op de verzameling reële x- en y-waarden, en i2 =-1.
Het nieuwe concept heft alle beperkingen op het gebruik van een algebraïsche functie op en lijkt op een grafiek van een rechte lijn in coördinaten van reële en imaginaire waarden.
Complex vliegtuig
De geometrische vorm van complexe getallen stelt ons in staat om veel van hun eigenschappen visueel weer te geven. Op de Re(z)-as markeren we de reële x-waarden, op de Im(z) - de denkbeeldige waarden van y, dan zal het z-punt op het vlak de vereiste complexe waarde weergeven.
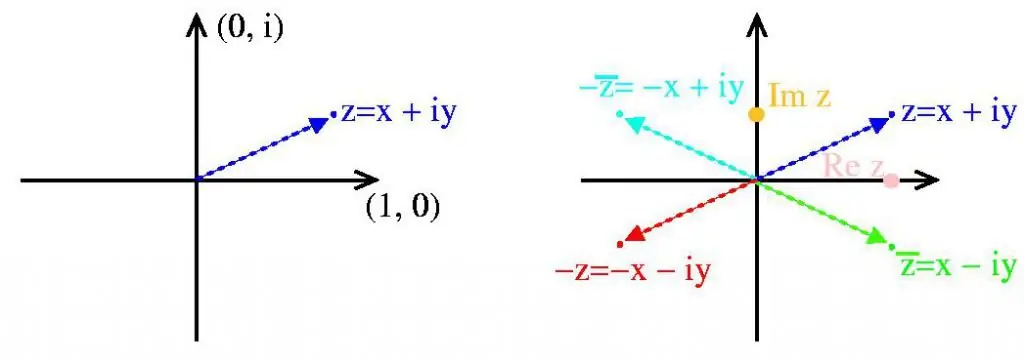
Definities:
- Re(z) - reële as.
- Im(z) - betekent de denkbeeldige as.
- z - voorwaardelijk punt van een complex getal.
- De numerieke waarde van de lengte van de vector van nul tot z wordt genoemdmodule.
- Reële en denkbeeldige assen verdelen het vliegtuig in vieren. Met een positieve waarde van de coördinaten - ik kwart. Wanneer het argument van de reële as kleiner is dan 0, en de denkbeeldige as groter is dan 0 - II kwart. Als de coördinaten negatief zijn - III kwartaal. Het laatste, vierde kwartaal bevat veel positieve reële waarden en negatieve denkbeeldige waarden.
Zo kan men op een vlak met x- en y-coördinaatwaarden altijd een punt van een complex getal visualiseren. Het karakter i wordt geïntroduceerd om het echte deel van het denkbeeldige te scheiden.
Eigenschappen
- Als de waarde van het denkbeeldige argument nul is, krijgen we alleen een getal (z=x), dat zich op de reële as bevindt en bij de reële verzameling hoort.
- Speciaal geval wanneer de waarde van het reële argument nul wordt, komt de uitdrukking z=i×y overeen met de locatie van het punt op de denkbeeldige as.
- De algemene vorm van z=x + i×y is voor niet-nulwaarden van de argumenten. Geeft de locatie aan van het punt dat het complexe getal karakteriseert in een van de kwartalen.
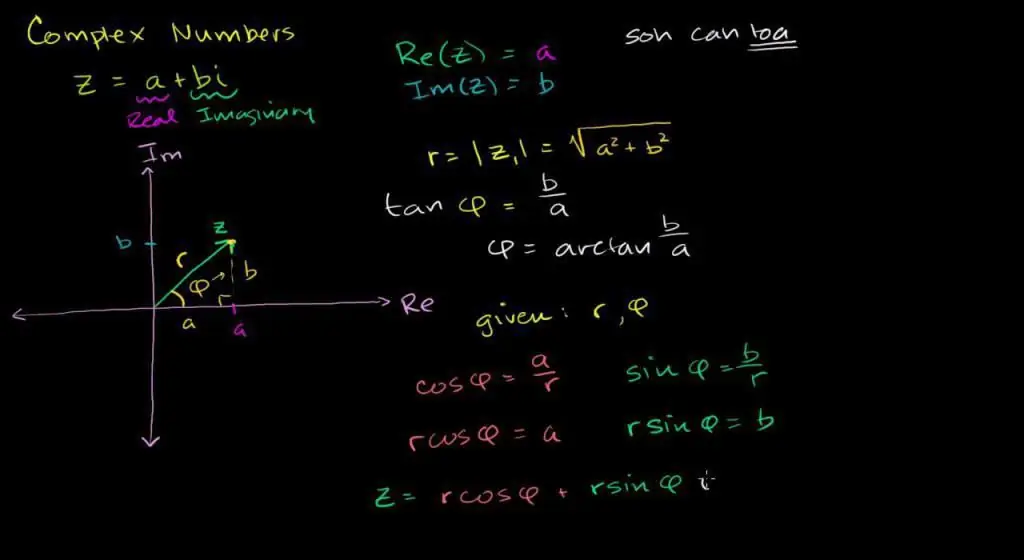
Trigonometrische notatie
Herinner je het poolcoördinatenstelsel en de definitie van de trigonometrische functies sin en cos. Het is duidelijk dat het met behulp van deze functies mogelijk is om de locatie van elk punt op het vlak te beschrijven. Om dit te doen, volstaat het om de lengte van de polaire bundel en de hellingshoek tot de reële as te kennen.
Definitie. Een invoer van de vorm ∣z ∣ vermenigvuldigd met de som van de trigonometrische functies cos(ϴ) en het imaginaire deel i ×sin(ϴ) wordt een trigonometrisch complex getal genoemd. Hier is de aanduiding de hellingshoek ten opzichte van de reële as
ϴ=arg(z) en r=∣z∣, straallengte.
Uit de definitie en eigenschappen van trigonometrische functies volgt een zeer belangrijke Moivre-formule:
zn =r × (cos(n × ϴ) + i × sin(n × ϴ)).
Met deze formule is het handig om veel stelsels van vergelijkingen met trigonometrische functies op te lossen. Vooral wanneer het probleem van het verheffen tot een macht zich voordoet.
Module en fase
Om de beschrijving van een complexe verzameling compleet te maken, stellen we twee belangrijke definities voor.
Als je de stelling van Pythagoras kent, is het gemakkelijk om de lengte van de straal in het poolcoördinatenstelsel te berekenen.
r=∣z∣=√(x2 + y2), zo'n notatie op een complexe ruimte wordt een " module" en karakteriseert de afstand van 0 tot een punt op het vlak.
De hellingshoek van de complexe bundel ten opzichte van de echte lijn ϴ wordt gewoonlijk de fase genoemd.
De definitie laat zien dat de echte en imaginaire delen worden beschreven met behulp van cyclische functies. Namelijk:
- x=r × cos(ϴ);
- y=r × sin(ϴ);
Omgekeerd is de fase gerelateerd aan algebraïsche waarden via de formule:
ϴ=arctan(x / y) + µ, correctie µ wordt ingevoerd om rekening te houden met de periodiciteit van geometrische functies.
Euler-formule
Wiskundigen gebruiken vaak de exponentiële vorm. Complexe vlakke getallen worden geschreven als uitdrukkingen
z=r × ei×ϴ , die volgt uit de Euler-formule.

Dit record wordt veel gebruikt voor de praktische berekening van fysieke grootheden. Vorm van presentatie in de vormexponentiële complexe getallen zijn vooral handig voor technische berekeningen, waarbij het noodzakelijk wordt om circuits met sinusvormige stromen te berekenen en het noodzakelijk is om de waarde van integralen van functies met een bepaalde periode te kennen. De berekeningen zelf dienen als hulpmiddel bij het ontwerpen van verschillende machines en mechanismen.
Bewerkingen definiëren
Zoals al opgemerkt, zijn alle algebraïsche wetten van het werken met wiskundige basisfuncties van toepassing op complexe getallen.
Som bewerking
Bij het toevoegen van complexe waarden worden hun reële en imaginaire delen ook toegevoegd.
z=z1 + z2 waarbij z1 en z2 - algemene complexe getallen. Het transformeren van de uitdrukking, na het openen van de haakjes en het vereenvoudigen van de notatie, krijgen we het echte argument x=(x1 + x2), het denkbeeldige argument y=(y 1 + y2).
In de grafiek lijkt het op de optelling van twee vectoren, volgens de bekende parallellogramregel.
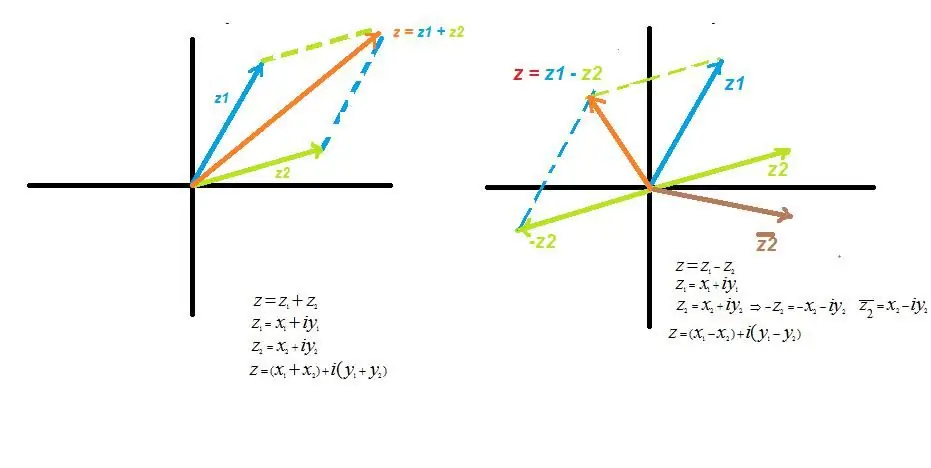
Aftrekken
Beschouwd als een speciaal geval van optellen, wanneer een getal positief is, is het andere negatief, dat wil zeggen, gelegen in het spiegelkwartier. Algebraïsche notatie lijkt op het verschil tussen echte en imaginaire delen.
z=z1 - z2, of, rekening houdend met de waarden van de argumenten, vergelijkbaar met de toevoeging bewerking, verkrijgen we voor de reële waarden x=(x1 - x2) en denkbeeldige y=(y1- y2).
Vermenigvuldiging op het complexe vlak
Met behulp van de regels voor het werken met veeltermen leiden we de formule afom complexe getallen op te lossen.
Volg de algemene algebraïsche regels z=z1×z2, beschrijf elk argument en som gelijkaardige op. De echte en imaginaire delen kunnen als volgt worden geschreven:
- x=x1 × x2 - y1 × y2,
- y=x1 × y2 + x2 × y 1.
Het ziet er mooier uit als we exponentiële complexe getallen gebruiken.
De uitdrukking ziet er als volgt uit: z=z1 × z2 =r1 × eiϴ1 × r2 × eiϴ2=r1 × r2 × ei(ϴ1+ϴ2).
Verder eenvoudig, de modules worden vermenigvuldigd en de fasen worden toegevoegd.
Divisie
Als we de bewerking van deling beschouwen als de inverse van vermenigvuldiging, krijgen we een eenvoudige uitdrukking in exponentiële notatie. Het delen van de waarde z1 door z2 is het resultaat van het delen van hun modules en faseverschil. Formeel ziet het er bij gebruik van de exponentiële vorm van complexe getallen als volgt uit:
z=z1 / z2 =r1 × e iϴ1 / r2 × ei ϴ2=r1 / r2× ei(ϴ1-ϴ 2).
In de vorm van algebraïsche notatie is de bewerking van het delen van de getallen van het complexe vlak iets gecompliceerder geschreven:
z=z1 / z2.
Beschrijven van argumenten en uitvoeren van polynomiale transformaties, het is gemakkelijk om waarden te krijgenx=x1 × x2 + y1 × y2, respectievelijk y=x2 × y1 - x1 × y2 , echter, binnen de beschreven ruimte, is deze uitdrukking zinvol als z2 ≠ 0.
Extract de wortel
Al het bovenstaande kan worden toegepast bij het definiëren van complexere algebraïsche functies - verheffen tot een willekeurige macht en inverse daarvan - het extraheren van de wortel.
Als we het algemene concept van verheffen tot de macht n gebruiken, krijgen we de definitie:
zn =(r × eiϴ).
Gebruik gemeenschappelijke eigenschappen, herschrijf als:
zn =rn × eiϴ.
We hebben een eenvoudige formule om een complex getal tot een macht te verheffen.
Uit de definitie van de graad halen we een heel belangrijk gevolg. Een even macht van de denkbeeldige eenheid is altijd 1. Elke oneven macht van de denkbeeldige eenheid is altijd -1.
Laten we nu de inverse functie bestuderen - de wortel extraheren.
Laten we voor het gemak van de notatie n=2 nemen. De vierkantswortel w van de complexe waarde z op het complexe vlak C wordt beschouwd als de uitdrukking z=±, geldig voor elk reëel argument groter dan of gelijk aan nul. Voor w ≦ 0 is er geen oplossing.
Laten we eens kijken naar de eenvoudigste kwadratische vergelijking z2 =1. Gebruik complexe getalformules en herschrijf r2 × ei2ϴ =r2 × ei2ϴ=ei0. Uit het record blijkt dat r2 =1 en ϴ=0, daarom hebben we een unieke oplossing gelijk aan 1. Maar dit is in tegenspraak met het idee dat z=-1 ook past in de definitie van een vierkantswortel.
Laten we uitzoeken waar we geen rekening mee houden. Als we ons de trigonometrische notatie herinneren, herstellen we de verklaring - met een periodieke verandering in de fase ϴ verandert het complexe getal niet. Laat p de waarde van de punt aangeven, dan hebben we r2 × ei2ϴ =ei(0+p), vandaar 2ϴ=0 + p, of ϴ=p / 2. Daarom, ei0 =1 en eip/2 =-1. We hebben de tweede oplossing, die overeenkomt met het algemene begrip van de vierkantswortel.
Dus, om een willekeurige wortel van een complex getal te vinden, volgen we de procedure.
- Schrijf de exponentiële vorm w=∣w∣ × ei(arg (w) + pk), k is een willekeurig geheel getal.
- Het gewenste getal wordt ook weergegeven in de Euler-vorm z=r × eiϴ.
- Gebruik de algemene definitie van de wortelextractiefunctie r ei ϴ =∣w∣ × ei(arg(w) + pk).
- Van de algemene eigenschappen van de gelijkheid van modules en argumenten, schrijven we rn =∣w∣ en nϴ=arg (w) + p×k.
- Het definitieve record van de wortel van een complex getal wordt beschreven door de formule z=√∣w∣ × ei ( arg (w) + pk ) / .
- Opmerking. De waarde van ∣w∣ is per definitieis een positief reëel getal, dus de wortel van elke graad is logisch.
Veld en vervoeging
Tot slot geven we twee belangrijke definities die van weinig belang zijn voor het oplossen van toegepaste problemen met complexe getallen, maar essentieel zijn voor de verdere ontwikkeling van de wiskundige theorie.
Er wordt gezegd dat de uitdrukkingen voor optellen en vermenigvuldigen een veld vormen als ze voldoen aan de axioma's voor alle elementen van het complexe vlak z:
- De complexe som verandert niet door het wisselen van plaats van complexe termen.
- De bewering is waar - in een complexe uitdrukking kan elke som van twee getallen worden vervangen door hun waarde.
- Er is een neutrale waarde 0 waarvoor z + 0=0 + z=z waar is.
- Voor elke z is er een tegengestelde - z, waarvan de toevoeging nul oplevert.
- Bij het veranderen van de plaats van complexe factoren, verandert het complexe product niet.
- De vermenigvuldiging van twee willekeurige getallen kan worden vervangen door hun waarde.
- Er is een neutrale waarde 1, vermenigvuldiging waarmee het complexe getal niet verandert.
- Voor elke z ≠ 0 is er een inverse van z-1, die vermenigvuldigt met 1.
- De som van twee getallen vermenigvuldigen met een derde is gelijk aan de bewerking van elk van hen vermenigvuldigen met dit getal en de resultaten optellen.
- 0 ≠ 1.
De getallen z1 =x + i×y en z2 =x - i×y heten conjugaat.
Stelling. Voor vervoeging is de bewering waar:
- De vervoeging van de som is gelijk aan de som van de geconjugeerde elementen.
- De vervoeging van het product isproduct van vervoegingen.
- De vervoeging van vervoeging is gelijk aan het getal zelf.
In de algemene algebra worden zulke eigenschappen veldautomorfismen genoemd.
Voorbeelden
Door de gegeven regels en formules van complexe getallen te volgen, kunt u er gemakkelijk mee werken.
Laten we eens kijken naar de eenvoudigste voorbeelden.
Probleem 1. Gebruik de vergelijking 3y +5 x i=15 - 7i om x en y te bepalen.
Beslissing. Denk aan de definitie van complexe gelijkheden, dan 3y=15, 5x=-7. Daarom, x=-7 / 5, y=5.
Taak 2. Bereken de waarden 2 + i28 en 1 + i135.
Beslissing. Het is duidelijk dat 28 een even getal is, uit de consequentie van de definitie van een complex getal in de macht hebben we i28 =1, wat betekent dat de uitdrukking 2 + i 28 =3. De tweede waarde, i135 =-1, dan 1 + i135 =0.
Taak 3. Bereken het product van de waarden 2 + 5i en 4 + 3i.
Beslissing. Uit de algemene eigenschappen van vermenigvuldiging van complexe getallen verkrijgen we (2 + 5i)X(4 + 3i)=8 - 15 + i(6 + 20). De nieuwe waarde is -7 + 26i.
Taak 4. Bereken de wortels van de vergelijking z3 =-i.
Beslissing. Er zijn verschillende manieren om een complex getal te vinden. Laten we een van de mogelijke overwegen. Per definitie is ∣ - i∣=1, de fase voor -i is -p / 4. De oorspronkelijke vergelijking kan worden herschreven als r3ei3ϴ =e-p/4+pk, waarbij z=e-p / 12 + pk/3, voor elk geheel getal k.
De oplossingenset heeft de vorm (e-ip/12,eip/4, ei2 p/3).
Waarom hebben we complexe getallen nodig
De geschiedenis kent veel voorbeelden waarin wetenschappers, die aan een theorie werken, niet eens nadenken over de praktische toepassing van hun resultaten. Wiskunde is in de eerste plaats een spel van de geest, een strikte naleving van oorzaak-en-gevolgrelaties. Bijna alle wiskundige constructies worden gereduceerd tot het oplossen van integraal- en differentiaalvergelijkingen, en die worden op hun beurt, met enige benadering, opgelost door de wortels van veeltermen te vinden. Hier stuiten we voor het eerst op de paradox van denkbeeldige getallen.
Wetenschappers, natuuronderzoekers, die volledig praktische problemen oplossen, hun toevlucht nemen tot oplossingen van verschillende vergelijkingen, ontdekken wiskundige paradoxen. De interpretatie van deze paradoxen leidt tot absoluut verbazingwekkende ontdekkingen. De dubbele aard van elektromagnetische golven is zo'n voorbeeld. Complexe getallen spelen een cruciale rol bij het begrijpen van hun eigenschappen.
Dit heeft op zijn beurt praktische toepassing gevonden in optica, radio-elektronica, energie en vele andere technologische gebieden. Een ander voorbeeld, veel moeilijker om fysieke verschijnselen te begrijpen. Antimaterie werd voorspeld op het puntje van een pen. En pas vele jaren later beginnen de pogingen om het fysiek te synthetiseren.
Denk niet dat er alleen in de natuurkunde zulke situaties bestaan. Niet minder interessante ontdekkingen worden gedaan in dieren in het wild, in de synthese van macromoleculen, tijdens de studie van kunstmatige intelligentie. En dat is allemaal te danken aanverruiming van ons bewustzijn, weg van het simpele optellen en aftrekken van natuurlijke waarden.






