Zoals je weet, behoort elke fysieke hoeveelheid tot een van de twee typen, het is ofwel scalair of vector. In dit artikel zullen we kinematische kenmerken als snelheid en acceleratie beschouwen, en ook laten zien waar de versnellings- en snelheidsvectoren naartoe zijn gericht.
Wat is snelheid en acceleratie?
Beide hoeveelheden die in deze paragraaf worden genoemd, zijn belangrijke kenmerken van elke vorm van beweging, of het nu gaat om het verplaatsen van een lichaam in een rechte lijn of langs een gebogen pad.
Snelheid is de snelheid waarmee coördinaten in de loop van de tijd veranderen. Wiskundig gezien is deze waarde gelijk aan de afgeleide naar de tijd van de afgelegde afstand, dat wil zeggen:
v¯=dl¯/dt.
Hier is de vector l¯ gericht vanaf het beginpunt van het pad naar het eindpunt.
Acceleratie is op zijn beurt de snelheid waarmee de snelheid zelf in de tijd verandert. In de vorm van een formule kan het als volgt worden geschreven:
a¯=dv¯/dt.
Uiteraard nemen we de tweede afgeleide vanverplaatsingsvector l¯ in de tijd krijgen we ook de waarde van de versnelling.
Aangezien snelheid wordt gemeten in meters per seconde, wordt versnelling, volgens de geschreven uitdrukking, gemeten in meters per seconde in het kwadraat.

Waar zijn de versnellings- en snelheidsvectoren?
In de natuurkunde wordt elke mechanische beweging van een lichaam meestal gekenmerkt door een bepaald traject. De laatste is een denkbeeldige curve waarlangs het lichaam in de ruimte beweegt. Een rechte lijn of een cirkel zijn bijvoorbeeld uitstekende voorbeelden van veelvoorkomende bewegingspaden.
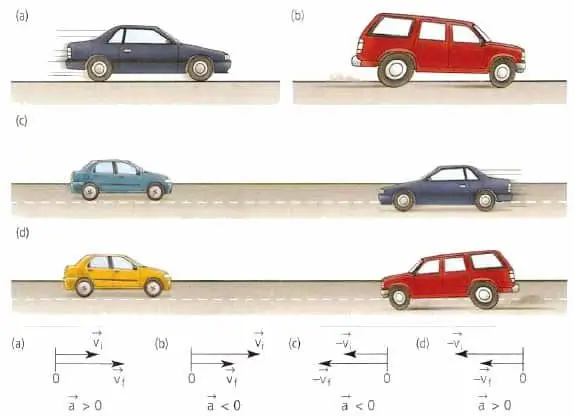
De snelheidsvector van het lichaam is altijd gericht in de bewegingsrichting, ongeacht of het lichaam vertraagt of versnelt, of het nu in een rechte lijn of langs een bocht beweegt. In geometrische termen gesproken, is de snelheidsvector tangentieel gericht op het punt van het traject waarin het lichaam zich momenteel bevindt.
De versnellingsvector van een materiaal- of lichaamspunt heeft niets te maken met snelheid. Deze vector is gericht in de richting van snelheidsverandering. Voor rechtlijnige beweging kan de waarde a¯ bijvoorbeeld samenvallen met v¯ of tegengesteld zijn aan v¯.
Kracht die inwerkt op het lichaam en versnelling
We hebben ontdekt dat de versnellingsvector van het lichaam is gericht op de verandering van de snelheidsvector. Het is echter niet altijd eenvoudig om te bepalen hoe de snelheid verandert op een bepaald punt in het traject. Om de verandering in snelheid te bepalen, is het bovendien noodzakelijk om de bewerking uit te voerenvectorverschillen. Om deze moeilijkheden bij het bepalen van de richting van de vector a¯ te vermijden, is er een andere manier om er snel achter te komen.
Hieronder staat de beroemde en bekende wet van Newton voor elke student:
F¯=ma¯.
De formule laat zien dat de oorzaak van versnelling in lichamen de kracht is die erop inwerkt. Aangezien de massa m een scalair is, zijn de krachtvector F¯ en de versnellingsvector a¯ in dezelfde richting. Dit feit moet worden onthouden en in de praktijk worden toegepast wanneer het nodig is om de richting van de hoeveelheid te bepalen a¯.
Als er verschillende krachten op het lichaam werken, dan is de richting van de versnellingsvector gelijk aan de resulterende vector van alle krachten.
Cirkelbeweging en versnelling
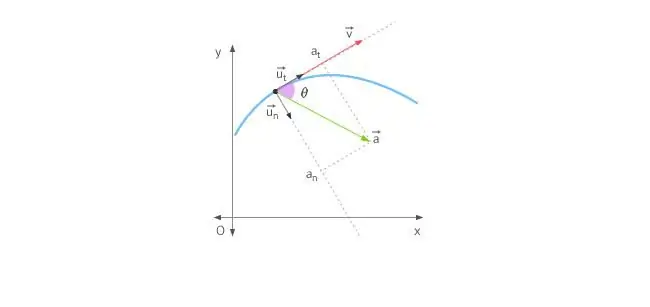
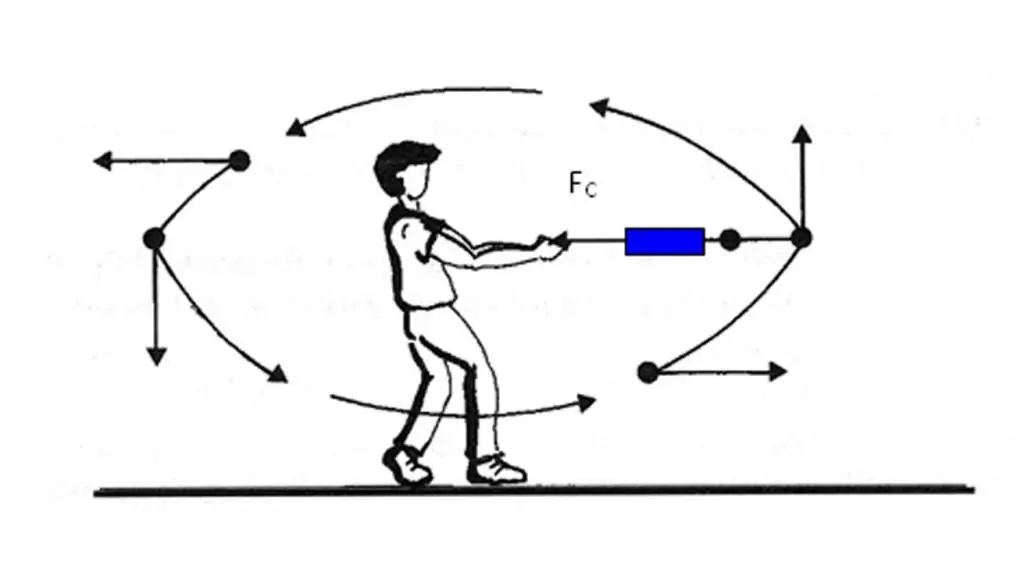
Als een lichaam in een rechte lijn beweegt, is de versnelling naar voren of naar achteren gericht. In het geval van beweging in een cirkel wordt de situatie gecompliceerd door het feit dat de snelheidsvector constant van richting verandert. Gezien het bovenstaande wordt de totale versnelling bepaald door zijn twee componenten: tangentiële en normale versnellingen.
Tangentiële versnelling is precies hetzelfde gericht als de snelheidsvector, of ertegenin. Met andere woorden, deze versnellingscomponent is gericht langs de raaklijn aan het traject. Tangentiële versnelling beschrijft de verandering in de modulus van de snelheid zelf.
Normale versnelling is gericht langs de normaal op het gegeven punt van het traject, rekening houdend met de kromming ervan. In het geval van cirkelvormige beweging geeft de vector van deze component aan:naar het midden, dat wil zeggen, de normale versnelling is gericht langs de rotatiestraal. Dit onderdeel wordt vaak centripetaal genoemd.
Volledige versnelling is de som van deze componenten, dus de vector kan willekeurig worden gericht ten opzichte van de cirkellijn.
Als het lichaam roteert zonder de lineaire snelheid te veranderen, dan is er alleen een normaalcomponent die niet nul is, dus de volledige versnellingsvector is gericht naar het middelpunt van de cirkel. Merk op dat dit centrum ook wordt beïnvloed door een kracht die het lichaam op zijn baan houdt. De zwaartekracht van de zon houdt bijvoorbeeld onze aarde en andere planeten in hun banen.






