Versnelling en snelheid zijn twee belangrijke kinematische kenmerken van elk type beweging. Als u de afhankelijkheid van deze grootheden in de tijd kent, kunt u de door het lichaam afgelegde weg berekenen. Dit artikel bevat het antwoord op de vraag hoe je de versnelling kunt vinden, de snelheid en tijd kennen.
Het concept van snelheid en acceleratie
Voordat we een antwoord geven op de vraag hoe, snelheid en tijd kennen, versnelling vinden, laten we elk van de kenmerken bekijken vanuit het oogpunt van natuurkunde.
Snelheid is een waarde die de snelheid van verandering van coördinaten in de ruimte bepa alt wanneer het lichaam beweegt. De snelheid wordt berekend met de formule:
v=dl/dt.
Waar dl het pad is dat door het lichaam wordt afgelegd gedurende de tijd dt. De snelheid is altijd gericht langs de raaklijn in het bewegingspad.
Beweging kan plaatsvinden met een constante snelheid in de tijd of met een variabele snelheid. In het laatste geval spreken we van de aanwezigheid van versnelling. In de natuurkunde bepa alt versnelling de veranderingssnelheid van v, die wordt geschreven als een formule:
a=dv/dt.
Deze gelijkheid is het antwoord op de vraag hoe te vindensnelheid acceleratie. Om dit te doen, volstaat het om de eerste afgeleide van v.
te nemen
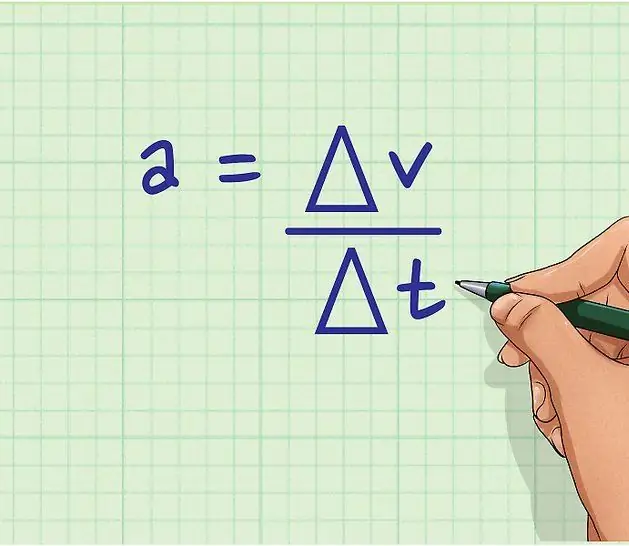
De richting van de versnelling v alt samen met de richting van het verschil in de snelheidsvectoren. Bij rechtlijnige versnelde beweging zijn de grootheden a en v in dezelfde richting gericht.
Hoe vind je acceleratie gegeven snelheid en tijd?
Bij het bestuderen van mechanica beschouwen we eerst uniforme en uniform versnelde soorten beweging langs een recht traject. In beide gevallen moet het tijdsinterval Δt worden gekozen om de versnelling te bepalen. Vervolgens moeten de waarden van de snelheden v1 en v2 aan het einde van dit interval worden bepaald. De gemiddelde versnelling wordt als volgt gedefinieerd:
a=(v2- v1)/Δt.
Bij eenparige beweging blijft de snelheid constant (v2=v1), dus de waarde van een wil nul zijn. In het geval van een eenparig versnelde beweging, zal de waarde a constant zijn, dus het hangt niet af van het tijdsinterval Δt in de formule.
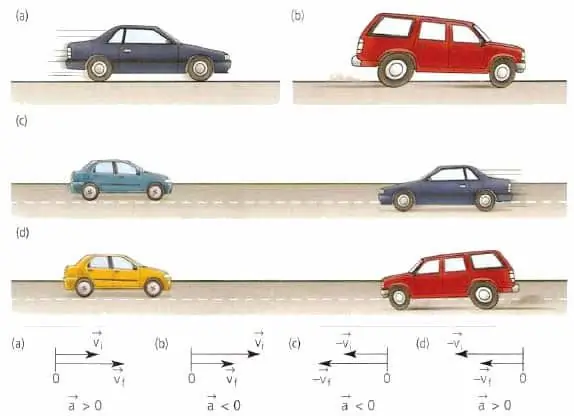
Voor meer complexe gevallen van beweging, wanneer de snelheid een functie van de tijd is, moet je de formule gebruiken voor a tot en met de afgeleide, die in de paragraaf hierboven werd gepresenteerd.
Voorbeeld van probleemoplossing
Na de vraag hoe we de versnelling kunnen vinden, de tijd en snelheid kennende, zullen we een eenvoudig probleem oplossen. Stel dat het lichaam, dat zich langs een bepaald traject beweegt, van snelheid verandert in overeenstemming met de volgende vergelijking:
v=3t2- t + 4.
Wat is de versnelling van het lichaam op tijdstip t=5 seconden?
De versnelling is de eerste afgeleide van v met betrekking tot de variabele t, we hebben:
a=dv/dt=6t - 1.
Om de vraag van het probleem te beantwoorden, moet u de bekende waarde van tijd in de resulterende vergelijking vervangen: a=29 m/c2.






