Een lineaire functie is een rechte lijn die langs een oppervlak wordt getrokken. Het kan worden onderverdeeld in verschillende soorten en modellen. Hieronder zullen we de formules bekijken om het te verkrijgen, evenals het bereiken van de perfectie in het vlak. In de tekeningen kunt u dit volledig verifiëren en begrijpen hoe het eruit zou moeten zien.
Lineaire functie y=kx + b
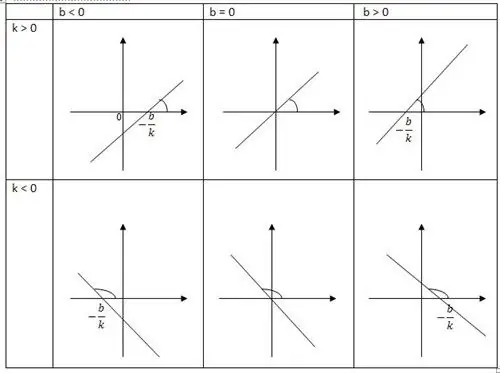
Deze waarde is een nauwkeurige meting van een variabele in één weergave. Increment verwijst naar de basiseigenschap van een lineaire functie, het wordt evenredig met het verhoogde argument. Met andere woorden, de functie vertegenwoordigt een veralgemening van directe evenredigheid. Een rechte lijn is een grafiek van een lineaire functie. Hier komt zijn naam vandaan. Een reële variabele raakt een andere reële functie.
Eigenschappen
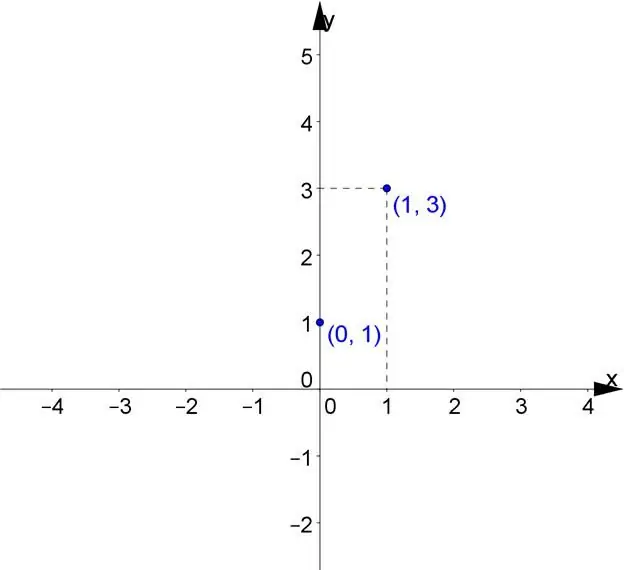
Lineaire functie is een generatrix van een rechte lijn, die een positieve richting van de x-as heeft. Een van de bepalende hellingsfactoren is k, het bepa alt de tangens van de hoek a. De rechte lijn gevormd in de positieve richting van de x-as is k. De andere coördinaat b geeft aanpuntcoördinaten, evenals het snijpunt van de lijn met de as.
Wat zijn niet-lineaire functies?
Functies die niet lineair zijn, worden niet-lineair genoemd. Dit is een wiskundige relatie tussen variabelen. Niet-lineaire enen kunnen niet worden uitgedrukt als y=ax + b. Deze term wordt gebruikt op die momenten dat het nodig is om de algemene casus te bestuderen. Dit proces begint met de lagere graden. In dit geval worden kwadratische correcties overwogen. Zo'n functie heeft een continue kromming.
De beschouwde niet-lineaire vergelijking is willekeurig. Een voorbeeld van een niet-lineaire functie is y=x2. Vaak worden de termen "lineaire functie" gebruikt, met een verfijning en toevoeging van "homogeen". Het kan worden toegepast op een exacte lineaire afbeelding van X, wat een vectorruimte is. Een lineaire functie is het hele systeem zoals het.






